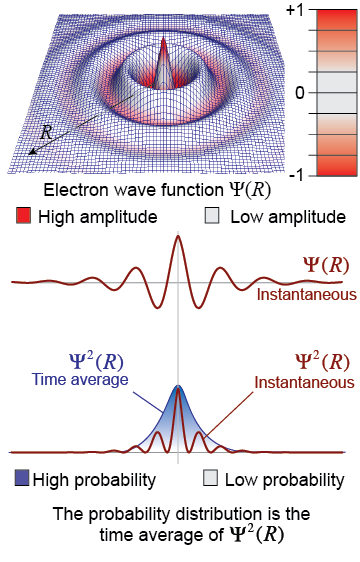
|
In 1926, Austrian physicist Erwin Schrödinger proposed that a quantum electron can be described by a wave function Ψ(R). The wave function is a three-dimensional description of the electron’s amplitude over space. The wave function has positive and negative values and can interfere with itself or other wave functions. Every characteristic of the electron can be determined from its wave function, including its momentum, energy, and position. 
| 
|
|
To determine the probability of finding the electron in a given region of space, you calculate the square of the wave function, Ψ2, over that region. The time average of Ψ2 is the probability. The blue-shaded region under the graph of Ψ2 is the probability distribution of the electron in that region of space.
|
|
Schrödinger’s equation describes how the wave function interacts with matter and energy. The equation is essentially a quantum expression of the conservation of energy. We include it because it is beautiful in a very deep way once you learn to read the language in which it is written. You are not expected to solve it in this course! You will learn how to use it in a college course in quantum physics.
|
|
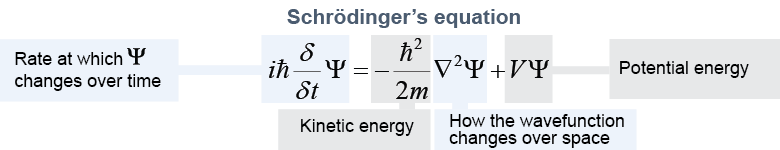
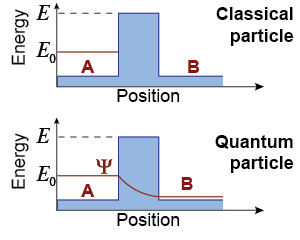Consider the position versus energy diagram on the right. In classical physics, a particle with energy E0 cannot get from point A to point B. A quantum particle, however, can tunnel through the barrier even if it does not have enough energy! The wave function decreases in amplitude but does not vanish in areas of space where energy conservation is violated. Tunneling occurs when the energy barrier is “thin” enough that the wave function still has some amplitude on the other side. An electron with energy E0 has a finite probability of being found at point B.
|
| |
|
