|
Erwin Schrödinger proposed the fundamental equation of quantum mechanics in 1926. When Schrödinger’s equation is applied to the atom, the result is a family of different solutions. Each solution corresponds to one allowable quantum state for an electron and is characterized by four quantum numbers. Each quantum state in the atom has a unique “quantum address” of the four quantum numbers, n, l, m, and s. The principal quantum number n is the one that appears in Balmer’s formula. 
|
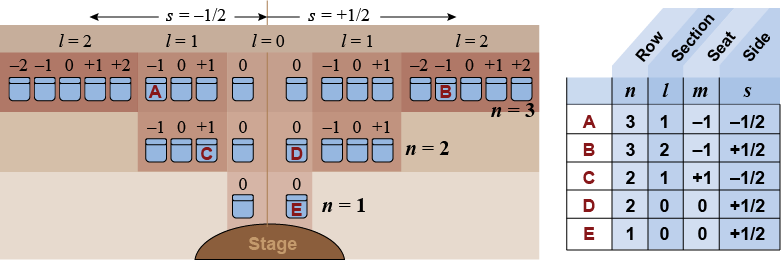
Think of an atom like a multilevel theater where each seat can hold up to one person. The best seats are closest to the stage but there are a limited number. The quantum numbers are the address code for each seat. The principal quantum number n tells you the row. The last number, s, tells you whether the seat is on the right or left side. The number l tells you what section and m is a specific seat in that section. 
|
|
Like the seats in our imaginary auditorium, every quantum state in the atom is identified by a unique combination of the four quantum numbers. The orbital angular momentum quantum number, l, can only be a positive integer from zero to n − 1. For example, if n = 1, the only possibility is l = 0. If n = 2, then l can be 0 or 1. The magnetic quantum number, m, is an integer that can go from −l to +l. For example, if l = 2, then m can have any of five values between −2 and +2: m = −2, −1, 0, 1, or 2. The last quantum number, s, is the electron spin angular momentum. An electron can have only one of two different spin states, up (+½) or down (−½). 
|
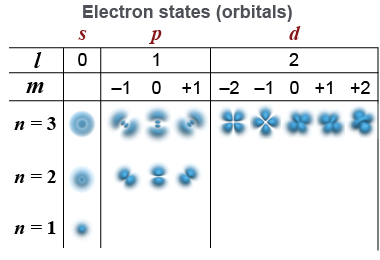
| All the electrons in the atom are attracted to the nucleus but repelled from each other. This dance of attraction and repulsion creates complex three-dimensional shapes for each electron “orbital.” The orbital angular momentum and magnetic quantum numbers determine the spatial shape. When l = 0 the orbital is spherically symmetric. When l = 1 there are three perpendicular states along each of the coordinate axes. The l = 0, 1, 2, and 3 states correspond to the s, p, d, and f orbital notation in chemistry. |

|
| |
|

