|
When we observe a baseball, we see light that hits the baseball and reflects from it into our eyes. How do we “see” an electron? On the quantum level, observing is not so straightforward. If we detect an electron by scattering a photon from it, we disturb the electron, so it moves off in an unknown direction. In fact, any act of “observing” on the quantum level disturbs the very system we are trying to observe, changing it in random ways. In 1927, the German physicist Werner Heisenberg asked the following: Is it possible to know simultaneously both the momentum and the position of an electron? 
|
|
Heisenberg’s answer is the uncertainty principle, which states that no possible means of measurement can simultaneously determine momentum and position to better than the limits of equation (26.4).
|
| (26.4) | | | Δp | = | uncertainty of momentum measurement (kg m/s) | | Δx | = | uncertainty of position measurement (m) | | h | = | Planck’s constant = 6.63×10−34 J s |
| Uncertainty
principle
|
|
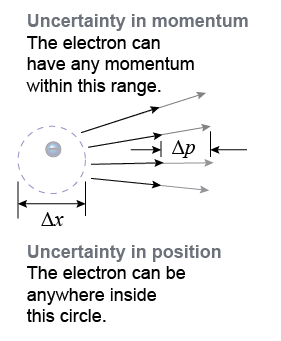The quantities Δx and Δp are the uncertainties in position and momentum. By uncertainty, we mean that a measurement of position that is 100% accurate has zero uncertainty: Δx = 0. Equation (26.4) tells us that it is not possible to know the position and momentum of a quantum particle to any accuracy better than ΔpΔx ≥ h/4π. The more accurately we know a particle’s momentum (Δp = small), the less we can know about the particle’s position (Δx = large). This is not because we need better measurements! The uncertainty principle says that the quantum universe is fundamentally unpredictable when it comes to single particles.
 |
The reason why in the macroscopic world we do not concern ourselves with the implications of the uncertainty principle has to do with the smallness of Plank’s constant.
For example, if the speed of a 100 g ball and an electron are measured to be the same, say 100 km/hr, and have the same uncertainty of 0.1%, what is the uncertainty in the measurement of their positions?
To solve this problem we must calculate Δp for the ball and the electron and then use Heisenberg’s uncertainty relationship to calculate Δx for the ball and the electron.
For the electron, For the ball, The uncertainty in the measurement of the position is now calculated from the relationship The maximum accuracy with which we can calculate the position of the electron is The maximum accuracy with which we can calculate the position of the ball is 
|
The uncertainty principle can also be written in terms of the energy measurement and the time that it takes to perform this measurement. | (26.5) | | | ΔE | = | uncertainty of energy measurement (J) | | Δt | = | uncertainty of time measurement (s) | | h | = | Planck’s constant = 6.63×10−34 J s |
| Uncertainty in
energy and time
|
|
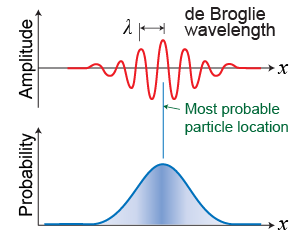The uncertainty principle starts to make sense when you think about a particle as a wave. What does the idea of “position” of a wave mean? Heisenberg’s principle pointed toward probability as the meaning of de Broglie’s matter waves. Where the wave amplitude is largest, you have the highest probability of finding the particle if you did an experiment that looked for it. But “highest probability” does not mean 100%. Because the wave is distributed over space, there is a nonzero probability of finding the electron anywhere that its matter wave has significant amplitude.
|
