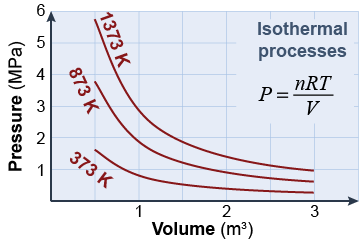|
An isothermal process is a change in pressure and volume in which temperature is kept constant. In this case, pressure and volume are inversely related to each other. If pressure increases, volume decreases and vice versa. The diagram shows isothermal processes at different temperatures for an ideal gas. Although not quite achievable in a real engine, isothermal heat transfer has the highest possible theoretical efficiency. 
 |
Heat may be transferred in an isothermal process when the constant temperature of the gas is less than the temperature of the surroundings. Imagine a heat reservoir at temperature Th in contact with a slightly cooler gas. As the gas absorbs heat, it is also allowed to expand by doing work on the piston. The gas temperature stays constant because some of the added heat is transformed into work instead of raising the temperature. 
|
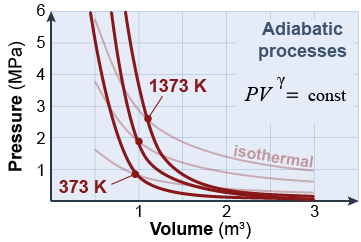Another important ideal is an adiabatic process in which zero heat is exchanged. A process that occurs very quickly, such as a gas expanding rapidly, is approximately adiabatic because there is not enough time for much heat to flow in or out. A process that takes place in a perfectly insulated container is also adiabatic. The diagram shows that adiabatic processes change pressure more rapidly than isothermal processes.
|
|
On a pressure–volume graph, an adiabatic process is a curve with a shape different from that of the isothermal curve. The adiabatic relationship between pressure and volume is given by equation (25.3).
|
| (25.3) | | | P | = | pressure (Pa) | | V | = | volume (m3) | | γ | = | ratio of specific heats = cp/cv |
| Adiabatic process
|
|
|
In equation (25.3), the quantity γ is the ratio of specific heats, γ = cp/cv. As you learned on page 685, cp is the specific heat at constant pressure and cv is the specific heat at constant volume.
|
|
In the last section, we learned that adiabatic processes are reversible because no heat flows, making the change in entropy (Q/T) equal to zero. Reversibility is the “zero friction” limit of efficiency. The ideal heat engine should therefore use reversible processes as much as possible.
|
|
Adiabatic and isothermal processes are important because an ideal heat engine can be modeled by two isothermal curves and two adiabatic curves. This thermodynamic cycle, called the Carnot cycle, has the highest possible theoretical efficiency of any heat engine that operates by changing the pressure, volume, and temperature of a gas. All real heat engines have efficiencies less than that of the ideal Carnot cycle. The cycle was discovered by the French engineer Sadi Carnot in 1824. For this work, Carnot is recognized as the “father” of the science of thermodynamics.
|
