Essential Physics

Specific heat of an ideal gas


How does a gas store thermal energy?	When heat is added to a gas, the particles move faster and the temperature increases. One way to look at this is to envision the gas as storing thermal energy in the motion of its constituent atoms. In fact, all matter stores thermal energy in a similar way. Specific heat is another macroscopic property that can be derived from statistical mechanics and particle motion.
Constant pressure vs. constant volume	For a gas there is a difference between adding heat at constant pressure and adding heat at constant volume. If pressure is constant, then volume changes and some of the heat energy becomes work since PΔV ≠ 0. The specific heat at constant pressure has the symbol c_p. In contrast, if heat is added at constant volume, then no work is done and all the energy goes to changing pressure. The specific heat at constant volume has the symbol c_v.
Deriving the specific heat	Consider one mole of gas, which contains 6.022 × 10²³ (N_A) particles. The mass is m_mol, the mass of one mole. The internal energy U of a monatomic gas of N_A particles is (3/2)N_Ak_BT. Set this equal to the heat Q it takes to raise the temperature of this mass by an amount ΔT: $\begin{matrix} heat & internal energy \\ Q = m_{m o l} c_{v} Δ T & U = \frac{3}{2} N_{A} k_{B} T & \to & m_{m o l} c_{v} Δ T = \frac{3}{2} N_{A} k_{B} T \end{matrix}$
The result	To be correct in setting these equal, the heat Q must be the amount to raise the temperature from absolute zero to T. In kelvins the temperature change is ΔT = T. Solve this for c_v, and the result is the specific heat at constant volume: $m_{m o l} c_{v} T = \frac{3}{2} N_{A} k_{B} T \to c_{v} = \frac{3}{2} \frac{N_{A} k_{B}}{m_{m o l}}$

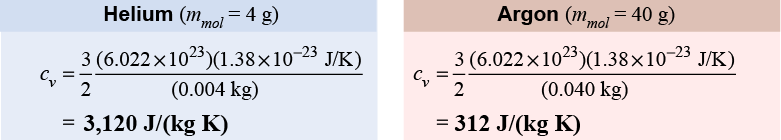
Comparing theory and experiment	These theoretical values are in excellent agreement with experimental measurements for helium and argon gases. The agreement between measured and predicted specific heat is strong evidence supporting the kinetic theory of matter. For air, however, the coefficient in front of the equations is 5/2 instead of 3/2. This is because air is 99% diatomic gases (O₂ and N₂). Each molecule can have kinetic energy of rotation around two axes as well as kinetic energy of translation along the three coordinate directions, which leads to the five degrees of freedom in the numerator of the coefficient 5/2.
The molar specific heat	Many books develop this same calculation in terms of the molar heat capacity (or molar specific heat), which has units of joules per mole per kelvin [or J/(mol K)] instead of joules per kilogram per kelvin. For this calculation, physicists traditionally use the fact that the product of Boltzmann’s constant and Avogadro’s number is the ideal gas constant R: R = N_A k_B Now equate the heat absorbed when changing the temperature (from absolute zero to T) with the thermal energy of one mole of particles: $m_{m o l} c_{v} T = \frac{3}{2} R T$ After canceling the temperature from both sides, we get an equation for c_v. To put this in terms of moles instead of kilograms, we use the ratio that one mole has a mass of m_mol: $c_{v} = \frac{3}{2} \frac{R}{m_{m o l}} \to c_{v} = \frac{3}{2} \frac{R}{m_{m o l}} (\frac{m_{m o l}}{m o l})$ Finally, we have a beautiful and elegant equation that says that the specific heat of any monatomic ideal gas is (3/2)R in J/(mol K): $c_{v} = \frac{3}{2} R$
Testing your knowledge	For an ideal gas, what does the specific heat at constant volume depend on? volume pressure temperature the mass of one mole
	Choice d is correct. The specific heat of an ideal gas at constant volume decreases with molar mass but does not depend on temperature, pressure, or volume.


		685