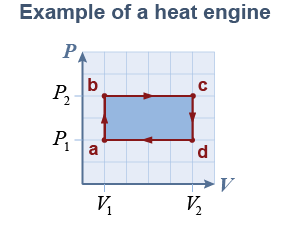Essential Physics

Efficiency of a heat engine


How much heat is required?	The efficiency of a heat engine is the ratio of work output divided by heat input. The process from a to b occurs at constant volume; the heat added, Q_ab, therefore depends on the moles of gas, the molar specific heat at constant volume, C_V, and the change in temperature. The process from b to c occurs at constant pressure, so the heat added, Q_bc, instead depends on the molar specific heat at constant pressure, C_P: $\begin{matrix} Q_{a b} = n C_{V} (T_{b} - T_{a}), & Q_{b c} = n C_{P} (T_{c} - T_{b}) \end{matrix}$
Molar specific heats	The equations above and below use the molar specific heat—which you learned about on page 670. Typical values for air are C_V = 20.8 J/(mol K) and C_P = 29.1 J/(mol K).
Temperature at each point in the cycle	Assume an ideal gas for which PV = nRT. The temperatures at points a, b, c, and d are therefore determined by the pressures and volumes: $\begin{matrix} T_{a} = \frac{P_{1} V_{1}}{n R}, & T_{b} = \frac{P_{2} V_{1}}{n R}, & T_{c} = \frac{P_{2} V_{2}}{n R}, & T_{d} = \frac{P_{1} V_{2}}{n R} . \end{matrix}$
Calculating input heat	After substituting for the temperatures we find the heat inputs Q_ab and Q_bc: $Q_{a b} = \frac{C_{v}}{R} V_{1} (P_{2} - P_{1}) Q_{b c} = \frac{C_{p}}{R} P_{2} (V_{2} - V_{1})$
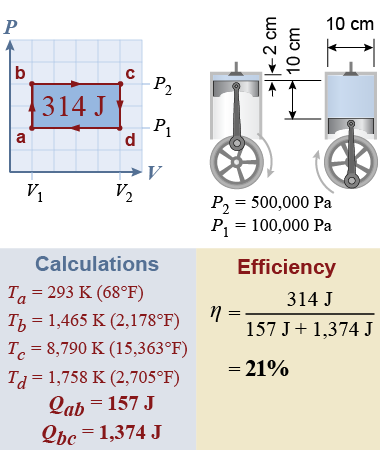How would this theoretical engine perform?	Consider a large car engine, in which each piston has a 10 cm diameter, stroke of 10 cm, and clearance of 2 cm and operates between 1 and 5 atmospheres (100,000 to 500,000 Pa). Apply the above equations to calculate the input heat as $Q_{a b} + Q_{b c} = 157 J + 1, 374 J = 1, 531 J .$ The work done in the thermodynamic process is the area inside the PV diagram, or $(P_{2} - P_{1}) (V_{2} - V_{1}) = 314 J .$ The input heat is almost five times the work output of the engine! Furthermore, to keep the pressure constant from b to c requires that the temperature be T_c = 15,363ºF! A real engine could not sustain this high a temperature.
Why is the efficiency so low?	This thermodynamic cycle has a terrible efficiency of 21%. Heat not converted to work is rejected to the surroundings during steps c → d and d → a. According to the first law, the heat rejected is the heat added minus the work done, or 1,271 J (79%). Soon we will see how to get better efficiency, but, according to basic thermodynamic principles, no heat engine operating above absolute zero can convert 100% of heat into output work.


740