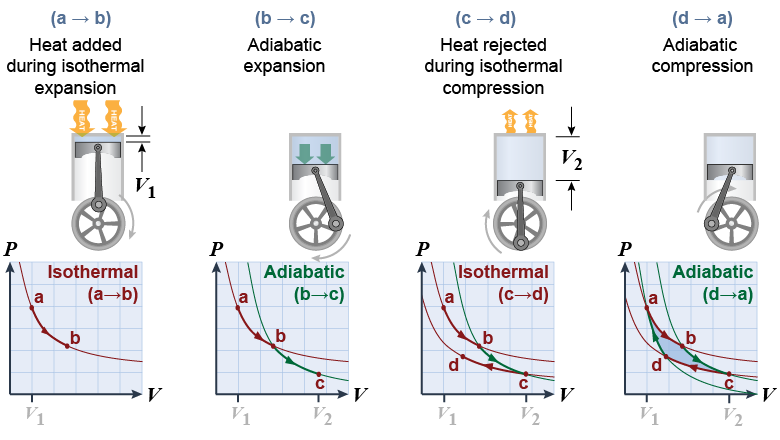
|
Consider an ideal-gas heat engine that uses a piston that starts at position a. - Heat is added and the gas is allowed to expand isothermally by converting some of the heat into work following the isothermal curve (a → b).
- The gas is then allowed to expand further adiabatically (b → c), thereby extracting more work by lowering the temperature. This is a frictionless, reversible change that extracts the most possible work from the expanding gas.
- Once the piston reaches its lowest point c the gas is compressed again but held to constant temperature along an isothermal curve (c → d). The heat generated by compression is transferred to the surroundings at the lower temperature Tc.
- The last step in the cycle is to compress the gas back to its starting point reversibly (d → a), for which Q = 0.
|
|
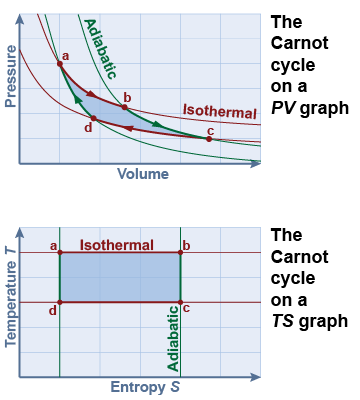The work done during the Carnot cycle is the shaded area on the PV graph, but this is difficult to calculate because of its curved shape. Instead, Carnot used the graph of temperature versus entropy (TS) to analyze this cycle. On the TS graph, area is equal to heat. An isothermal process is represented by a horizontal line (a → b). Because no heat flows (Q = 0), an adiabatic process is a vertical line (b → c) representing no change in entropy. The entire cycle is a rectangle on the TS graph defined by the two isothermal processes (a → b and c → d) and the two adiabatic processes (b → c and d → a).
|
| |
|
