|
The ideal gas law represents a connection between the microscopic motions of particles in a gas and their macroscopic quantities, such as temperature and pressure. How exactly does the ideal gas equation come about? To answer this question, we need to determine the average pressure on the sides of a container resulting from collisions of gas particles. 
|
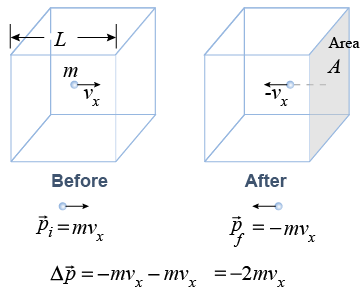Consider a particle traveling with velocity vx in the x-direction in a box of length L. The particle hits the side of the box, which has area A, and rebounds with velocity −vx.
Pressure is force divided by area. Force is the rate of change of momentum, F = ΔP/Δt. After colliding with the wall, the particle’s change in momentum is −2mvx.
|
|
The particle travels back and forth a distance 2L between collisions with the right-hand wall. The time it takes to traverse a distance of 2L is Δt = 2L/vx. The average force is therefore given by
|
|
The sign is negative because this is the force on the particle that changed its momentum. To calculate the pressure on the wall, we need the positive reaction force on the wall. The average pressure comes from this positive force divided by the area A of the wall: where we have used volume V = A × L. Note that PV is the kinetic energy associated with motion in the x-direction.
|
|
Next we need to relate vx to the average thermal speed vth. No one direction is favored over another in our imaginary box, so the average velocities in the x-, y-, and z-directions are equal. We can express this mathematically with vx2 = vy2 = vz2. The thermal speed vth, when broken into components, satisfies the relationship vth2 = vx2 + vy2 + vz2 = 3vx2, so we derive vx as a function of temperature T:
|
|
The last step is to substitute this relationship for vx. The result tells us that for a single particle PV = kBT. If the box contains N particles we have the ideal gas law, PV = NkBT. The ideal gas law comes directly from the addition of trillions of microscopic collisions among particles and their container. Thus the ideal gas law for a collection of N particles comes directly from the properties of a single particle.
|
