|
A gas for which pressure, temperature, and volume are steady and constant has a Maxwellian distribution of particle speeds. Knowing how many particles there are at any speed allows us to find the average thermal speed, which is the speed of a particle with average kinetic energy given by equation (23.5). This equation (repeated below) is derived directly from the Maxwellian distribution. 
 |
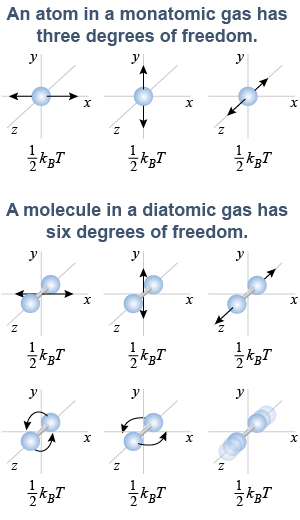In the quantum world, each independent way in which a particle can have energy constitutes one degree of freedom. Maxwell’s theory actually predicts that each degree of freedom has a thermal energy of (1/2)kBT. A single atom can move in three dimensions; therefore, it has three degrees of freedom, making its thermal energy (3/2)kBT. On the quantum level, rotating a single atom does not change its properties in any measurable way because a single atom is spherically symmetric. This means that rotation does not add degrees of freedom for a monatomic gas.
A diatomic molecule such as O2, however, has rotational symmetry about its long axis, but not around the other two axes perpendicular to it. This means that O2 molecules have two more degrees of freedom, corresponding to rotation about those two other axes. At sufficiently high temperatures an O2 molecule can also stretch along its long axis, adding a sixth degree of freedom.
Structure therefore allows a diatomic molecule to have five or six degrees of freedom depending on the temperature. The additional degrees of freedom mean that a quantity of oxygen gas stores more thermal energy at a given temperature when compared to the same quantity of a monatomic gas with similar mass per particle. 
|
| | | E | = | energy (J) | | kB | = | Boltzmann’s constant = 1.38×10−23 J/K | | T | = | absolute temperature (K) |
| Thermal energy
per atom
|
|
|
We determine the average thermal speed vth for a particle in a gas by setting the kinetic energy equal to the average thermal energy from equation (23.5): Solving this for the average thermal speed leads to the following equation.
|
| (23.13) | | | vth | = | thermal speed of particles (m/s) | | kB | = | Boltzmann’s constant = 1.38×10−23 J/K | | T | = | temperature (K) | | m | = | mass (kg) |
| Thermal speed
|
|
|
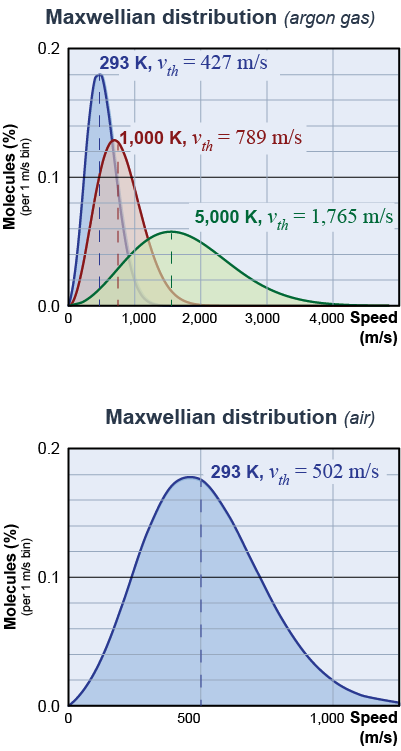
Argon is a monatomic gas that makes up about 1% of Earth’s atmosphere. Slightly heavier than oxygen or nitrogen, argon has an atomic mass of 40 g/mol. For argon gas at room temperature of 293 K (20ºC) the average thermal speed is 427 m/s, or 956 mph! As argon heats up, the average speed of the particles becomes even greater, reaching 1,765 m/s when the temperature is 5,000 kelvin!
| 
|
|
The thermal speed of air is higher than that of argon. Why? In equation (23.13), the thermal speed varies as the inverse square root of the mass of the particles. The average molecular mass of air (29 g/mol) is smaller than that for argon; therefore, the thermal speed of air is higher. At 293 K the average thermal speed of air is 502 m/s or 1,120 mph. The speed of sound is closely related to the thermal speed because sound waves are propagated by collisions between air molecules. In air, the speed of sound at 20ºC is 343 m/s and increases as the square root of the temperature, in agreement with the formula for the thermal speed.
|
Two different gases are at the same temperature. One is helium, which has an atomic mass of 4 g/mol. The other gas is neon, which has an atomic mass of 20 g/mol. Which of the following statements is true? - Helium atoms move faster because they have less mass and the same energy.
- Atoms of both helium and neon have about the same average speed because they have the same temperature.
- Helium atoms move slower because their mass is lower and therefore their energy is also lower.
- Neon atoms move faster because they have higher energy proportional to their higher mass.
 |
Choice a is correct. The average kinetic energy of both atoms is the same; therefore, helium atoms must move faster since they have less mass and equal energy compared to neon atoms. 
|
