|
Energy can be thought of as the ability to exert force and do work. Since force is pressure times area, energy and pressure are therefore closely related. One joule of work is done when a pressure of one pascal pushes a surface of one square meter a distance of one meter. The loss of energy by the fluid may lead to a decrease in temperature, pressure, or both. 
|
|
|
A pressure of one newton per square meter represents a potential energy density of one joule per cubic meter. Energy density has units of J/m3, analogous to mass density, which has units of kg/m3. The potential energy in a volume of fluid is therefore equal to its volume multiplied by its pressure.
|
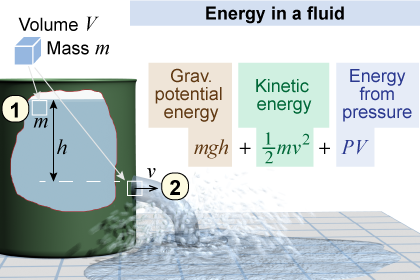To calculate the energy of a fluid, imagine a tank with a hole in the side through which a stream of water squirts. Pressure energy inside the tank is converted to kinetic energy when the water squirts out. The energy of a small mass m of water is the sum of the gravitational potential energy mgh (relative to the top of the tank), kinetic energy ½mv2, and potential energy from pressure, PV.
|
|
For fluids it is usually more convenient to use density ρ instead of mass. Divide the energy equation by volume V and the result is Bernoulli’s equation, which is given in equation (23.12). Bernoulli’s equation is the law of conservation of energy applied to the motion of a specific element of mass within the fluid that is moving along a streamline. A streamline is an imaginary line that follows the motion of a particular element of fluid as it moves.
|
|
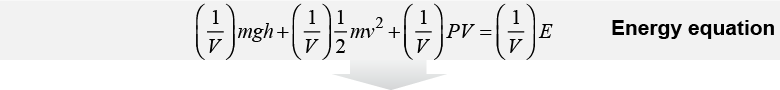
| (23.12) | | | ρ | = | density (kg/m3) | | g | = | gravitational acceleration | | | = | 9.8 N/kg | | h | = | height (m) | | v | = | speed (m/s) | | P | = | pressure (Pa or N/m2) |
| Bernoulli’s
equation
along a
streamline |
|
