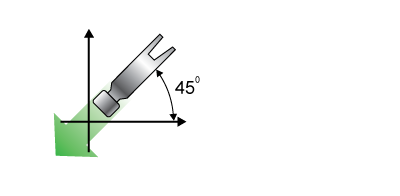
 Is the force of the hammer striking a board greater in the x- or y-direction when a hammer strike is directed at a 45° angle?
- Describe how to transform a force that is given in polar coordinates into a force of the same magnitude and opposite direction.
- Your teacher described the difference between displacement and distance. Based on your teacher’s statements, do you think there can be four displacements of equal distance that add up to no change in position? If so, then explain how this might be done.
- Explain what is different between two successive displacements of (0, 5) m and (5, 0) m and a single displacement of (5, 5) m?
- Describe the difference between how a compass defines angles and how angles are defined on the standard x–y graph you might find in a math book.
- Explain how the vector equation can represent one, two, or three equations.
- What does it mean when we claim that the x- and y-components of a velocity vector are independent of each other?
 Given that Newton’s second law is a vector equation, describe the relationship between the directions of force and acceleration that the second law implies.
- Is it possible for the acceleration vector and the velocity vector to be perpendicular to each other? If so, describe a situation where this might occur and the kind of motion that might result.
- Name a real-time technology that can generate a particle model chart that represents an object’s motion?
| | - Why do we choose the coordinate axes x and y to be horizontal and vertical instead of aligning them at the same angle as the initial velocity?
- In the absence of friction, explain why the horizontal component of a projectile’s velocity is a constant.
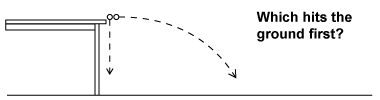
- One marble sits motionless at the edge of a table. A second marble is fired horizontally along the tabletop at the first one using a marble launcher. When the second marble strikes the first, one marble falls straight down and the other follows a curved path as shown in the diagram above. Compare when the two marbles hit the floor. Explain your reasoning.
- It is possible to adjust the angle of a ramp until a car just rolls down with constant speed and zero acceleration. Explain why there is no acceleration.
- How is carbon paper useful in collecting data in a projectile motion investigation?
- If Galileo’s descendants were to use a real-time technology to generate a ticker tape chart (such as on page 6) for constant velocity motion along a horizontal surface, then what would the chart look like?
- Name one or more advantages of using real-time technology—such as a ticker tape—instead of Galileo’s methods to generate a chart of motion down an inclined plane?
- Why is the trajectory of a soccer ball kicked in the air curved and not straight? Can you think of an example of projectile motion that does have a straight trajectory?
- A real-time graphing technology for a moving car, such as the ErgoBot, might measure the position of the wheels over time. How then does such as real-time system generate a chart of velocity versus time?
- Why is it useful to tilt the coordinate system to align with the angle of a ramp?
- When you add mass to a real car on a ramp, there is a measurable increase in acceleration. It is not large, maybe a few percent, but the effect is real and repeatable. Why?
 Consider a projectile launched upward at an angle between 0º and 90º from the horizontal. As the launch angle increases, what happens to the total time of flight for the projectile?
|
