|
You may have ridden a bicycle on a hill and noticed the substantial acceleration going down and the extra force required to go up. A hill is a natural example of an inclined plane, which is a flat but sloped surface also called a ramp. Because of the angle, a fraction of the object’s weight acts downward, along the ramp. The fraction increases as the angle increases and explains why you accelerate faster down a steep hill than a shallow one. The relationship between acceleration and ramp steepness is given in equation (6.11). 
|
| (6.11) | | | aramp | = | acceleration down the ramp (m/s2) | | h | = | vertical height of the ramp (m) | | L | = | distance along the ramp (m) | | g | = | acceleration due to gravity (m/s2) |
| Acceleration
down a ramp
|
|
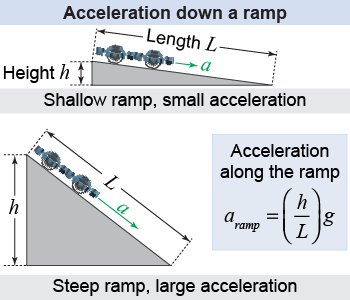If you ever drove over a high mountain pass, you probably saw signs on the descent warning truck drivers about high speeds. It may seem obvious, but trucks (and cars) can rapidly accelerate to high speeds on steep downhills if their drivers are not careful. The underlying phenomenon is found in the equation above: The acceleration due to gravity increases as the slope of the inclined plane (or ramp) increases. The slope of the hill is given by the ratio (h/L) in equation (6.11).
|
|
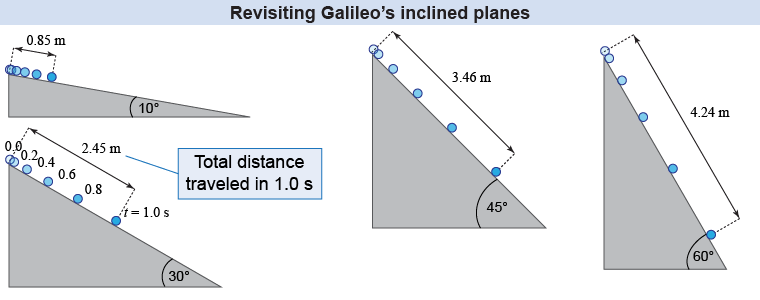
Galileo probably did not drop masses off the tower at Pisa to demonstrate the properties of gravitational acceleration. He did, however, construct inclined planes to do so! Why use ramps instead of dropped masses? Galileo did not have reliable time pieces available that could measure short time intervals. By using ramps, he slowed down the motion so that it could be measured accurately using his time pieces.
|
|
If we look back on Galileo’s experiments using a particle model illustrated above, we see that the total distance traveled per second increases as the ramp becomes steeper. Since the points are plotted every 0.2 s for all the ramps, the ball is moving fastest where the points are furthest apart. The ball is moving slower on the shallow ramp than on the steep ramp. Since we know that acceleration is the change in velocity per unit time, the acceleration must be larger along the steeper ramp.
 |
As you will learn later in Chapter 13, there is a difference in energy between a rolling ball and a sliding ball. Strictly speaking, the acceleration in the illustration above is for a ball sliding down a frictionless surface. If the ball were rolling down the ramp, then some of its gain in kinetic energy would be as rotational energy, not translational kinetic energy. As a result, it would not accelerate quite as quickly as shown in the illustration! 
|
Mazal took a board of length 1.193 m and tilted it so that one end was 0.129 m off the ground. She calculated that the acceleration along the ramp should be a = 1.06 m/s2. If she doubles the height of the same end of the board, what will be the new acceleration?
 |
From equation (6.11), the acceleration down the ramp is proportional to the height h. So when she doubles the height, she also doubles the acceleration to a = 2×1.06 m/s2 = 2.12 m/s2. 
|
