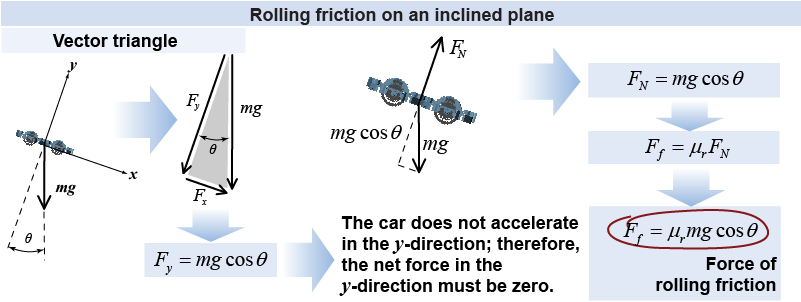
|
The inclined plane is an excellent laboratory for studying friction during motion, because the acceleration can easily be controlled by changing the angle. Consider a ramp that makes an angle θ with the horizontal. From the vector triangle, the normal force is the y-component of the car’s weight, or mg cos θ. 
|
|
|
The acceleration of the car is due to the net force acting parallel to the ramp. This includes the x-component of the car’s weight and rolling friction. You can see both forces in the equation for the net parallel force (below). The term with sin θ is the x-component of the car’s weight. The term μr cos θ is the effect of rolling friction. Applying Newton’s second law gives us an equation for the acceleration of the car. Friction lowers the acceleration of the car by g × μr cos θ.
|
|
| (6.13) | | | ax | = | acceleration along ramp (m/s2) | | g | = | acceleration of gravity = 9.8 m/s2 | | θ | = | ramp angle (degrees) | | μr | = | coefficient of rolling friction |
| Acceleration
with rolling friction |
|
|
Notice that the mass of the car does not appear in equation (6.13)! As with free fall, adding mass creates extra force from weight—but also increases inertia, which cancels out the effects of added weight. Similarly, rolling friction depends on the normal force and hence weight, so adding mass increases friction but does not change the acceleration.
|
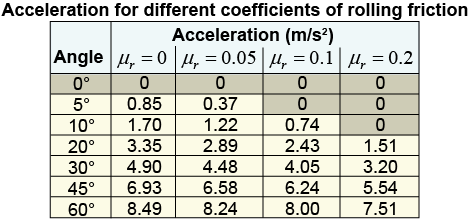The table on the right shows how the acceleration changes as the coefficient of rolling friction increases from 0.0 to 0.2. Notice that, when μr = 0.1, the car does not accelerate even at a ramp inclination angle of 5º. When μr = 0.2 the car does not start moving when on a ramp with an angle of 10°.
|
