| | Essential questions | | How is motion along each axis different for a projectile?
What are the shapes of position and velocity graphs for projectile motion? | |
|
Projectile motion occurs whenever a moving object is under no force except gravity. The equations of motion for each coordinate axis are different—and independent of each other—so you can analyze them separately. What projection angle will shoot a cannonball the farthest? 
|
Part 1: What angle launches projectiles the maximum distance?
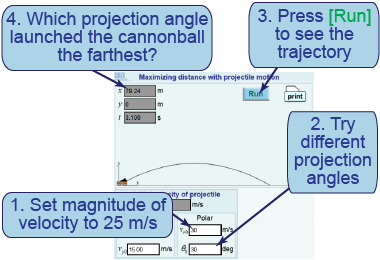
- Using your computer, click on the interactive simulation in the electronic resources to conduct the investigation. Set the magnitude of the velocity vr to 25 m/s.
- Try different projection angles, such as θ0 = 10°, 20°, 30°, and so on.
- For each, press [Run] to see the trajectory and inspect x to see how far it goes.
- What projection angle θ0 shoots the cannonball the furthest? Provide a conceptual explanation for why you think this angle always results in the furthest distance.
- Which component of velocity determines the time in the air?

|
On your computer, launch this interactive simulation using the button (on the left) in order to conduct the investigation. In this interactive simulation, you will launch a cannonball and try to hit a target. Change the components of the velocity (either in Cartesian coordinates or polar coordinates) and then enter [Run] to watch the projectile move in its trajectory. Vary the projection angle to determine what angle shoots the cannonball the furthest.
|
Part 2: Hitting a target with projectile motion
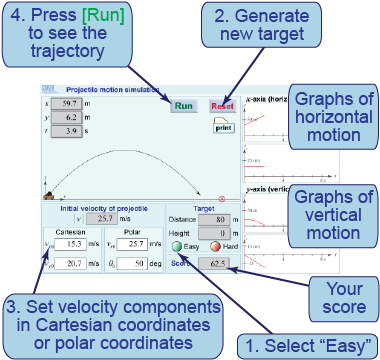
- Select “Easy” using the button.
- Press [Reset] to generate a new target.
- Set the components of the initial velocity using either Cartesian or polar coordinates.
- Press [Run] to see the trajectory. Modify the velocity as necessary to hit the target.
- Explain the difference between Cartesian and polar coordinates.
- Sketch the shapes of the graphs of x and vx versus time and y and vy versus time. Why do the graphs have these shapes?
- Select “Hard” and press [Reset] to generate an elevated target. Can you hit it?

|
In this interactive simulation, you will launch a cannonball and try to hit a target. Change the components of the velocity (either in Cartesian coordinates or polar coordinates) and then enter [Run] to watch the projectile move in its trajectory. A new target is randomly generated each time you enter [Reset].
|
Part 3: Projectile motion off the edge of a table
- Set carbon papers on a length of white craft paper on the floor next to a table.
- Roll a marble five times down a ramp (such as an inclined textbook) from the same starting point. Measure the vertical height and average horizontal distance traveled by the marbles through the air.
- Why is carbon paper useful for this investigation?
- Use the projectile motion equations to calculate the marble’s velocity when leaving the table.

| | |
| |
|

