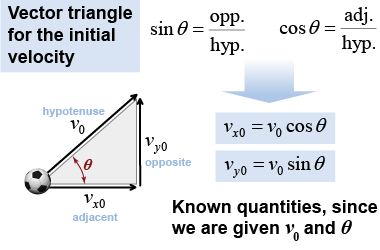|
Suppose a ball is kicked upward with an initial velocity of 10 m/s at an angle of 30° from the horizontal. How far does it travel before it hits the ground? At what angle of elevation should you kick the ball for it to reach the maximum distance? Both questions are answered by applying the equations of motion in two dimensions. The equations of motion are the same as before (equations 6.6 and 6.7), except that we are now given the magnitude of the initial velocity v0 instead of the individual velocity components. Using the projection angle, we get the initial individual velocity components of vx0 = v0 cos θ and vy0 = v0 sin θ, leading to the modified equations given below. 
|
| (6.8) | | | x | = | position in x-direction (m) | | v0 | = | initial speed (m/s) | | θ | = | projection angle (degrees) | | t | = | time (s) | | vx | = | velocity component in
x-direction (m/s) |
| Projectile motion
x-coordinate equations |
|
| (6.9) | | | y | = | position in y-direction (m) | | v0 | = | initial speed (m/s) | | θ | = | projection angle (degrees) | | t | = | time (s) | | vy | = | velocity component in
y-direction (m/s) |
| Projectile motion
y-coordinate equations |
|
|
The range of a projectile is the horizontal distance it covers before hitting the ground. That means x = v0t cos θ is the equation we want to solve. The initial speed v0 is known, and the angle θ is also known, while the time t is not known. So we use the y equations to solve for time t. The y-component equation for position is a quadratic, which means there are two solutions. Factoring the equation gives the following.
|
|
|
The first solution is for t = 0, which is when the ball is first kicked at the start. The second solution is the one we want because it describes the second time the ball touches the ground, from which we can determine the range we are looking for. Solving the second solution for time yields t = 2v0 sin θ0 / g. Substituting this into x = v0t cos θ yields the range equation:
|
| (6.10) | | | x | = | range (m) | | v0 | = | initial speed (m/s) | | θ | = | launch angle relative to horizontal | | g | = | acceleration of gravity (9.8 m/s2) |
| Range equation
|
|
What is the time for the ball to return to the ground when it is thrown directly upward at 18 m/s?
 |
Using t = x/v0 cos θ0 = 2v0 sin θ0/g and realizing that “upward” means that θ = 90°, we substitute values to get 
|
