|
How can we simplify these equations of motion for projectiles? We use the fact that gravity accelerates down; therefore, ay = –g and ax = 0! The equations of motion simplify a great deal because all the terms that include ax become zero. Also, to make the math simpler, we choose the initial position to be zero, so x0 = 0 m and y0 = 0 m. 
|
Let’s first examine the motion in the x-direction. Since there is no acceleration in x, the component of velocity in the x-direction is constant. The projectile moves with constant velocity along x! The x position changes linearly, as shown in equation (6.6). 
|
| (6.6) | | | x | = | position in x-direction (m) | | vx0 | = | initial velocity in x-direction (m/s) | | vx | = | velocity component in x-direction (m/s) | | t | = | time (s) |
| Projectile motion
x-component |
|
Now look at the equations of motion in the y-direction. The acceleration in y has a constant value of −g. As we learned in Chapter 4, constant (nonzero) acceleration results in velocity that changes linearly, as shown in equation (6.7). Position in the y-direction is a function of t and t2, as also shown in equation (6.7). 
|
| (6.7) | | | y | = | position in y-direction (m) | | vy0 | = | initial velocity in y-direction (m/s) | | vy | = | velocity component in y-direction (m/s) | | t | = | time (s) | | g | = | acceleration due to gravity = 9.8 m/s2 |
| Projectile motion
y-component |
|
Equations (6.6) and (6.7) are the equations of projectile motion when gravity is acting in the negative y-direction. The initial velocity given to the projectile—soccer ball, cannonball, etc.—has components vx0 in the x-direction and vy0 in the y-direction. 
|
|
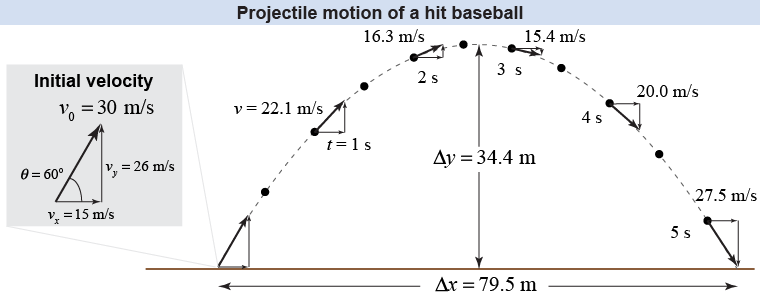
How do these equations work in a real-world example, such as a fly ball hit in a baseball game? Let’s assume the batter hits the ball somewhat upward with a velocity of 30 m/s and a projection angle of 60°. The ball’s initial velocity has components of 15 and 26 m/s in the x- and y-directions, respectively. Plugging these values into equations (6.6) and (6.7) results in the trajectory illustrated above—where we calculated the magnitude of the velocity using v2 = vx2 + vy2. 
|
In the illustration of the fly ball above, the position of the ball is depicted at fixed time intervals (every 0.5 s) to create a particle model of its motion. The ball positions are closest to each other at the top of the trajectory, which means that the speed is slowest there. The ball positions are furthest apart near the ground where the speed is fastest. 
|
When the baseball is first hit, its velocity has a position angle of 60° with the horizontal. After 2 s, what is the position angle of its velocity?
 |
From the illustration above, after 2 s the magnitude of the velocity is v = 16.3 m/s. We already know that the x-component of the velocity is constant at vx = 15 m/s, because there is no acceleration acting in the x-direction. Since we know the total velocity (the hypotenuse of the vector triangle) and the velocity in the x-direction, then we can get the position angle using the inverse cosine function: 
|

