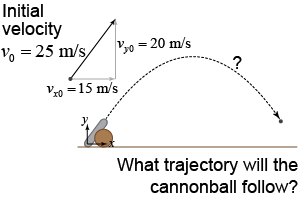|
Imagine you are firing a cannon, where the initial velocity has components vx0 = 15 m/s and vy0 = 20 m/s. What trajectory will the cannonball follow? To answer this question, we will use the equations of motion and graphs of the equations. For projectile motion of this cannonball, how do the equations of motion in the x-direction differ from the equations of motion in the y-direction? 
|
|
The basic difference is that gravity acts only in the y-direction, not in the x-direction. This is an important observation, because it means that motion is accelerated in the y-direction, but it is unaccelerated in the x-direction.
|
|
|
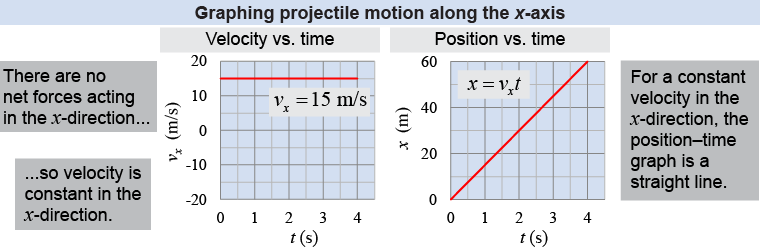
In the x-direction, there is no acceleration, so the velocity in the x-direction is constant at vx = 15 m/s, which is graphed above left. If vx is constant, then the position in the x-direction is given by x = vx0t = (15 m/s)t, which is a straight line graph of constant slope (above right).
|
|
|
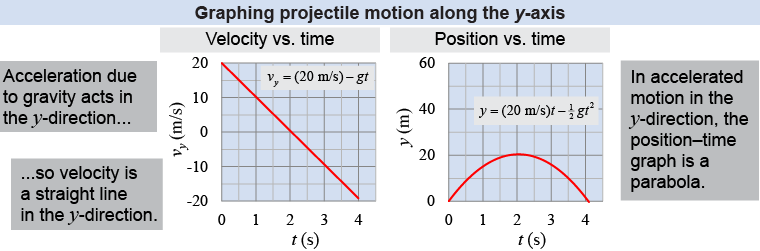
In the y-direction, the motion has a constant acceleration due to gravity g. The velocity is vy = vy0 − gt, which is a straight line of constant slope (above left). The position in the y-direction is y = vy0t − ½gt2, which is a parabola (above right).
|
|
These equations of motion and their graphs highlight a fundamental property of projectile motion: The position versus time graph in y is a parabola, whereas the same position versus time graph in x is a line.
|
How long does it take for a cannonball with initial velocity components vx0 = 15 m/s and vy0 = 20 m/s to hit the ground? (Hint: Analyze the y-direction equation of motion alone!)
 |
The initial velocity component in the y-direction is vy0 = 20 m/s. When the cannonball has returned to where it started, by symmetry the y velocity component will be −20 m/s. Since the acceleration is the change in velocity over the change in time, we can rearrange the acceleration to solve for time elapsed: An alternate solution appears on the bottom of the next page! 
|
