|
There are many situations in which the velocity of an object is a combination of two or more velocities. An example is a boat moving with a certain velocity relative to the water of a river. The water is moving with a different velocity. The velocity of the boat relative to the land is the sum of the boat’s velocity relative to the water plus the water’s velocity relative to the land. 
|
|
|
Velocity vectors are added by components, just like force and displacement vectors. Add the x-components separately and the y-components separately to calculate a resultant velocity. The illustrations above and below show the vector model of motion for velocity.
|
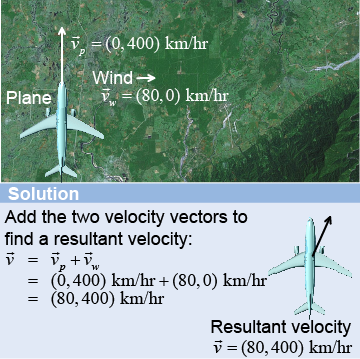Consider a commuter airplane flying due north with a velocity of 400 km/hr. A strong and steady high-altitude wind blows from the west at 80 km/hr. The resultant velocity of the plane is = (+80,+400) km/hr. Relative to the land, the plane is flying at an angle of 11.3° instead of true north. The effect of adding velocities is very real and a concern for anyone navigating a plane or boat. What is the actual speed of the plane with respect to the ground when the effect of the wind velocity is included? We calculate the magnitude of the net velocity (the speed) by drawing the vector triangle. The magnitude is given by the Pythagorean theorem v2 = vx2 + vy2.
|
|
|
Relative to the land, the plane is moving at a speed of 408 km/hr at a position angle of 11.3°. Because the component velocities add as squares, the actual speed of the plane is not that much greater than its northward component alone. If the pilot continued to steer straight north, however, then over a 2 hr flight the easterly displacement dx = vxt would be 160 km. She will miss the airport! What should she do to compensate?
|
What should the airplane pilot and the boat’s captain do to travel in their desired directions?
 |
In both cases, the pilots have to modify the direction of their vehicle’s velocity. The airplane pilot must steer a little bit westward into the wind, and the ship’s pilot must steer a little bit into the cross-current. 
|
