Using the thin lens formula
Real and virtual images in the equation Sign conventions for lenses
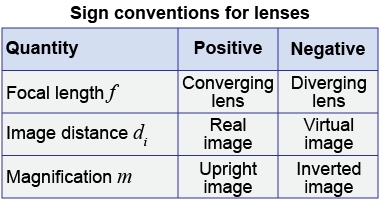
When using the thin lens formula in equation (21.3), a real image has a positive value of the image distance, i.e., di > 0. As you will see in the solved problem below, a virtual image is represented by a value of di < 0. A negative image distance means that the image is located on the same side of the lens as the object—the left-hand side of the illustrations above). As you learned on page 614, a virtual image cannot be projected onto a piece of paper.
Read the text aloud
Magnification and the thin lens formula In the previous chapter, we learned that the magnification of an image is the ratio of the image height to the object height. An alternate equation for the magnification is the negative of the ratio of the image distance to the object distance. Read the text aloud
Magnification from object and image distances
(21.4) m=− d i d o
m  = magnification
di  = image distance (m)
do  = object distance (m)
Magnification
alternate definition
Inverted images have negative magnification Why is there a minus sign in equation (21.4)? Look at the ray diagram for a convex lens on page 615. The image is inverted, which corresponds to the minus sign in equation (21.4). A negative magnification means that the image is inverted, whereas a positive magnification is an upright image. Read the text aloud Show Concave lenses and the thin lens formula
Virtual images and the thin lens formula A magnifying glass with a focal length of 20 cm is held 15 cm above the page of a book.
(a) How far from the lens is the image located? (b) Is the image real or virtual?
(c) What is the magnification of this image? (d) Is the image upright or inverted?
Asked: (a) image distance di; (b) whether image is real (di > 0) or virtual (di < 0); (c) magnification m of the image;
(d) whether the image is upright (m > 0) or inverted (m < 0)
Given: object distance do = 15 cm, focal length f = 20 cm
Relationships: 1 d i + 1 d o = 1 f ,   m=− d i d o
Solution: (a) Solve for 1/di in the thin lens formula and calculate: 1 d i = 1 f − 1 d o = 1 20 cm − 1 15 cm =(0.05−0.0667)  cm −1 =−0.0167  cm −1 Invert both sides of the equation to get di = 1/(−0.0167 cm−1) = −60 cm. (b) The image distance is negative, so this is a virtual image and it is therefore located on the same side as the object.
(c) Use the magnification equation:
m=− d i d o =− −60 cm 15 cm =+4
(d) The magnification is positive, so the image is upright.
Answer: (a) di = −60 cm. (b) It is a virtual image. (c) Magnification m = +4.
(d) It is an upright image.
Read the text aloud
Test your knowledge When a 20-cm-tall object is placed 40 cm from a lens, an image forms 60 cm from the lens on the other side. What is the magnification?
  1. −3/2
  2. −2/3
  3. 2/3
  4. 1/3
Show
Test your knowledge Consider the same 20-cm-tall object placed 40 cm from a lens, with an image forming 60 cm from the lens on the other side. What is the height of the image?
  1. −60 cm
  2. −30 cm
  3. −6.66 cm
  4. 13.33 cm
Show
618 Previous Page Next Page