| | Essential questions | | How do a microscope and telescope work? | |
|
The basic microscope and the telescope are each a compound optical device that uses two lenses. The object is imaged by the first (or objective) lens; this image is used as the object by the second (or eyepiece) lens. By choosing particular types of objective and eyepiece lenses, and by separating the two lenses by a suitable distance, both the microscope and the telescope can produce magnified images.
Caution: Never look directly at the Sun with either a microscope or a telescope! 
Part 1: Build a simple microscope
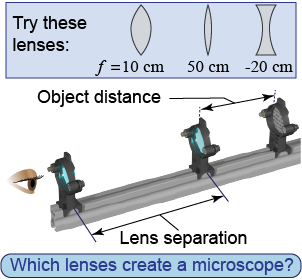
- Use three lenses (illustrated at right).
- Using two lenses at a time, determine which two lenses create a microscope by generating a magnified image of a nearby object.
- Construct a microscope on the optics track. Adjust the lens positions to improve the microscope magnification without significant distortion.
- What kinds of lenses are used to make a microscope?
- Which lens (if any) has a shorter focal length, the objective or eyepiece?
 |
Alternative way to mount lenses
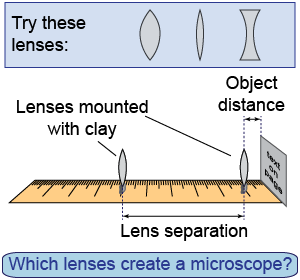The microscope can also be constructed by using a meter stick and clay for mounting the lenses. It is more difficult to achieve success with this method, however, because of the difficulty of aligning the optical axes of the two lenses with each other. 
|
Part 2: Model the simple microscope
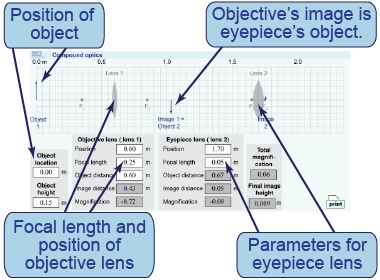
- Enter your microscope’s parameters into the compound optics simulation.
- Make small modifications to the positions of the lenses to see what range in positions produces a large magnification.
- Where is the object for the objective lens located relative to its focal point?
- Where is the eyepiece’s object located relative to its focal point?
- How is the separation of the lenses related to the focal lengths of the two lenses?
|
In this interactive simulation, you can create a compound optical system by combining two lenses. When the focal length of a lens is f > 0, it is a convex lens; when f < 0, it is a concave (or diverging) lens. With two lenses you can construct a microscope or telescope, but each may require a different choice of lenses for the objective and eyepiece. You can enter the position of the object; the telescope images a far-away object, whereas the microscope images a nearby one.
|
Magnification of a microscope
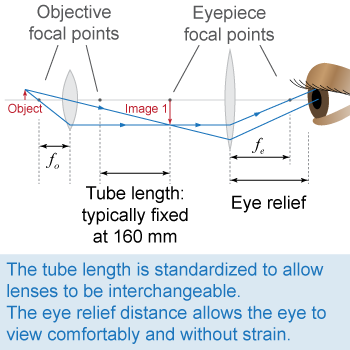Microscopes constructed as scientific instruments are designed to have fixed tube lengths of 160 mm. The standard close focus distance (the nearest object on which the eye can comfortably focus) is usually taken as 25.4 cm (10 in). The standardization in microscope dimensions allow either the objective or the eyepiece to be interchangeable. With these standardized distances, the magnification of a microscope is | | | m | = | magnification | | fo | = | objective's focal length (m) | | fe | = | eyepiece's focal length (m) |
| Magnification
of a microscope
|
The eye relief is the distance between the eye and the eyepiece lens, which must allow space for the viewer's eyelashes and eyeglasses; it is often 5–10 mm, but can be as high as 20 mm. The eye relief distance has two important purposes: It reduces strain on the eye by allowing the eye’s lens to focus at infinity (rather than the near field) and it allows the full light from the exit aperture of the eyepiece to be viewed by the eye. The further the viewer’s eye is located away from the eyepiece, the smaller will be the field size seen by the eye, so increasing the eye relief is not always desirable.
|
Part 3: Build and model a simple telescope
- Use the same lenses as in Part 1. Holding two lenses at a time—one at arms length and the other somewhat close to your eye—determine which two lenses can create a telescope that magnifies a distant object.
- Construct your telescope on the optical track.
- Devise a method to measure its magnification for a particular eye position.
- What kinds of lenses are used to make a Galilean telescope? A Keplerian telescope?
- Which lens (if any) has a shorter focal length, the objective or the eyepiece?
|
Part 4: Correcting human vision using eyeglasses
Use the compound optics simulation to represent the human eye with a convex lens (with a focal length of 1.7 cm) and corrective lenses (eyeglasses) with either a convex or a concave lens. The amount that eyeglasses change the path of light through them is measured in diopters, which is the inverse of the focal length (measured in meters). The diopter has the equivalent unit of m−1. Human eye and corrective lenses | | | Lens 1
(corrective lens) | Lens 2
(human eye) | | | Object
location
(m) | Lens
position
(m) | Focal
length
(m) | Lens
position
(m) | Focal
length
(m) | Image
distance
(m) | | No eyeglasses | 1.0 | 1.22 | 999 | 1.25 | 0.017 | | Weak reading glasses
(2.0 diopter) | 1.0 | 1.22 | 0.5 | 1.25 | 0.017 | | Strong reading glasses
(3.5 diopter) | 1.0 | 1.22 | 0.286 | 1.25 | 0.017 | | | Diverging lens eyeglasses | 1.0 | 1.22 | −0.286 | 1.25 | 0.017 | | - Use the interactive element to simulate each of the cases above. A focal length of 999 m is used in the first entry to represent no corrective lenses.
- Set up the optics track to study the effect of using corrective lenses. Use the f = 10 cm convex lens to represent the human eye and two pairs of reading eyeglasses (2.0 diopter and 3.5 diopter).
- With no “corrective lenses,” set the object distance at 20 cm and measure the image position.
- Place each pair of eyeglasses in front of the lens and measure the image position for each.
- How does the image distance change when you insert corrective lenses in front of the human eye?
- How does a concave corrective lens change the image distance differently from a convex corrective lens?
- Based on how corrective lenses change the image distance, what do you think are the problems in imaging formation called “nearsightedness” and “farsightedness”?
| | |
| |
|
