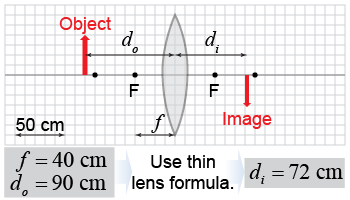|
Different kinds of lenses produce different image properties: real or virtual, upright or inverted, and magnified or reduced. Each configuration also produces an image at a particular location. How can you predict the location of an image? The relationship between the object distance do, the image distance do, and the focal length f of the lens is called the thin lens formula. If you know two of these quantities, you can use the thin lens formula to calculate the third quantity. Equation (21.3) is also called the Gaussian lens formula. 
 |
A thin lens means that the vertical size of the lens is much larger than its thickness. The thin lens formula is an approximation for the properties of a lens and the images it produces in the limit as it becomes infinitely thin. The lens in the illustration above is drawn somewhat on the thick side for visual clarity, but you should imagine that it is much thinner! 
|
| (21.3) | | | do | = | object distance (m) | | di | = | image distance (m) | | f | = | focal length (m) |
| Thin lens formula
|
|
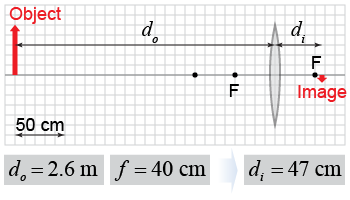What happens to the location of the image when the object is moved further and further away from the lens? As you can see in the figure at right, when the object is moved to do = 260 cm—which is 6.5 times larger than the focal length of the lens—the image is located slightly beyond the far focal length. As the object is placed further and further away from the lens—as the object distance “goes to infinity”—its images will be produced closer and closer to the focal point.
|
|
A general feature of convex lenses is that when the object distance becomes large (it “goes to infinity”) the image will be located at the far focal point. This property comes right out of the thin lens equation: When do becomes very large, then 1/do becomes very small because it is the reciprocal quantity. At that point, 1/f = 1/di, or di = f, which means that the image distance equals the focal length. Telescopes are optical devices designed to take images of objects that are located at infinity.
|
A student has a convex lens but does not know its focal length. She sets up a light source 75 cm in front of the lens and then uses an index card to determine that it produces an image on the other side of the lens 37.5 cm away from the lens. What is the focal length of the lens? | Asked: | focal length f of the lens | | Given: | Object distance do = 75 cm; image distance di = 37.5 cm | | Relationships: | | | Solution: | Insert the values into the thin lens equation: | |
Now take the inverse of both sides of equation to solve for focal length: | | Answer: | The focal length is 25 cm. |
|
An object is placed 3 m away from a converging lens with a focal length of 2 m. How far away from the lens will the image appear? - 0.5 m
- 1.2 m
- 2 m
- 6 m
 |
The correct answer is d.
Asked: image distance di
Given: object distance do = 3 m; focal length f = 2 m
Relationships: Solve: Rearrange and solve the equation for 1⁄di: Take the inverse of both sides to solve for di: 
|
|
If the object in the previous problem was placed north of the lens, on what side of the lens would the image appear?
|
|
The image would appear south of the lens. A positive image distance from the thin lens formula indicates that the image appears on the opposite side of the lens from the object. A negative distance indicates that the image appears on the same side.
|
|
Use the thin lens formula to prove that the location of the image in the first example on page 615 (the converging lens) is correct.
|
Asked: to apply the thin lens formula to the above diagram
Given: as interpreted from the diagram, object distance do = 15 units;
image distance di = 10 units; focal length f = 6 units
Relationships:
Solve: Insert values into the equation and check whether the values work: These values work, so the convex lens example is correct.
|
