| | Essential questions | | What law governs the energy transformations of motion on an inclined plane? | |
|
If you have ever skied down a mountain, biked down a hill, or ridden in a roller coaster, then you know that going downhill causes your speed to increase. The higher the hill, the faster you can go—up to a point. This investigation uses an interactive simulated hill to explore how gravitational potential energy and kinetic energy are used to explain the changes in motion. For example, if you want to design a roller coaster to reach 30 mph, how high must it be at the start? 
|
Part 1: Changes in energy for motion down an inclined plane
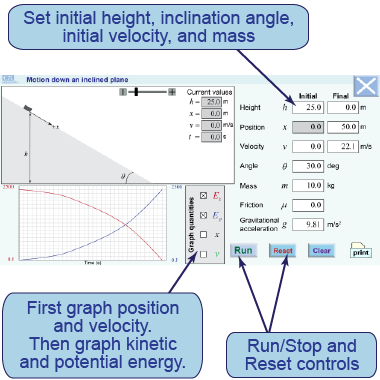
- Set the initial parameters for the interactive simulation of an inclined plane: θ = 15°, h0 = 100 m, x0 = v0 = μ = 0, and m = 20 kg.
- Press [Run] to watch the block slide down the ramp.
- Graph displacement and speed. What are the shapes of the graphs? Why do you get these shapes?
- Graph kinetic energy and potential energy. What are the shapes of the graphs? Why?
- What is the sum of the kinetic and potential energies at the top of the ramp when the block is released? At the bottom? How are their changes related to each other?
- What is the speed at the bottom of the ramp? Repeat for a few different values of the mass of the block. How does the speed change in each case? Why?
- Change the initial speed of the block to −20 m/s and +20 m/s. What is the change in kinetic energy at the bottom of the ramp? Explain why.

|
|
Use this interactive simulation of an inclined plane to do the investigations and answer these questions. You can change the angle of inclination of the inclined plane as well as the initial height and velocity of the ErgoBot. You can also choose which physical quantities to graph: displacement, velocity, kinetic energy, or gravitational potential energy.
|
Part 2: Designing a roller coaster that reaches 30 mph
- Convert 30 mph into units of m/s. Your goal is to make this the final speed of the block when it reaches the bottom of the ramp.
- Set the mass of the roller coaster to m = 2,000 kg.
- Vary the simulation parameters—such as the vertical height h0 or inclination angle θ—to produce a speed of 30 mph at the bottom of the ramp.
- The fastest roller coaster in the United States reaches a maximum speed of 128 mph. Use the interactive simulation to estimate the height of this roller coaster.
- How does changing the steepness of the roller coaster (while keeping the same initial height) affect the speed at the bottom of the ramp? Why?
- How does changing the mass of the roller coaster change its speed at the bottom? Why?
- Research the
actual height of the roller coaster in step #4. How well does your estimate agree with it? 
 |
Converting 30 mph into m/s
Since the interactive simulation uses meters per second, first we must convert 30 mph into meters per second. Start by converting 30 miles into meters: Then convert 1 hr into seconds: Finally, divide meters by seconds:A speed of 30 mph is therefore equivalent to a speed of 13.4 m/s. 
|
| |
|

