| | Essential questions | | Can energy conservation be used to predict the behavior of a system? | |
|
A system that includes a falling mass and a spring includes three forms of mechanical energy. By carefully modeling the flow of energy among potential, elastic, and kinetic forms, we can accurately predict how far a mass will drop before it is caught by the spring. 
|
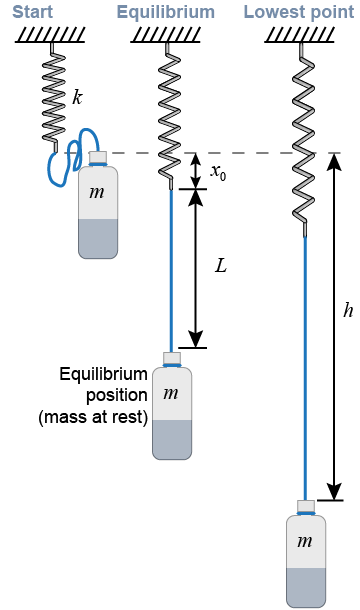You will need 250 g of water in a water bottle, tied to a string that allows the mass to drop about 1/2 m before it engages the extension spring (see the diagram). - Measure the mass of the water bottle and the length L of the string.
- Hold the spring against the wall and measure the free length and the extended length with the mass. This will allow you to determine the spring constant.
- Predict the total distance the mass falls when released from rest.
- Design an experimental procedure to measure the actual distance h that the mass falls, which equals the free fall distance L plus the maximum extension x of the spring.
- Write down an equation for the total energy in the system in terms of measureable variables, such as the string length and the water bottle mass.
- Use the data table to calculate the gravitational potential energy and elastic potential energy of the mass when it has fallen different distances.
- If the system is closed, approximately how far will the mass fall before it is stopped by the spring? How do you know? Use the table as your model to estimate the theoretical height the mass falls if the energy transformations are 100% efficient (and if the spring obeys Hooke’s law ideally).
- Record the experimental procedure you designed to measure the distance h. Identify the variables in your experiment. Which ones are controlled? What equipment did you select?
- Do the experiment using the measured value for the spring constant, mass, and string length. Calculate the efficiency of the overall energy transformation.
- Create a bar chart to display the kinetic, gravitational potential, and elastic potential energies at each of three locations: immediately after being released, when the spring just begins to extend, and when the bottle reaches its lowest point. How do you use relationships among these energies to determine the kinetic energy at each location?
- Use your model to predict the change in height that the mass falls if the mass were increased by 20%. Does the height change by 20%? Explain your reasoning using the predictions of your model. Conduct an experiment to test the model. Compare your actual results with your prediction.
- Prepare a written report for your investigation. In addition to addressing the above questions, describe the procedure, results, and conclusion or interpretation.
|
| |
|
