|
Friction often converts kinetic energy into forms that are not easily converted back into motion. Kinetic friction on a skidding car or a sliding baseball player acts to oppose the motion, transforming kinetic energy into unrecoverable heat. A skydiver acted on by air resistance and a swimmer subject to drag are also examples of systems that do work on their surroundings through the action of a frictional force, losing mechanical energy in the process. 
 |
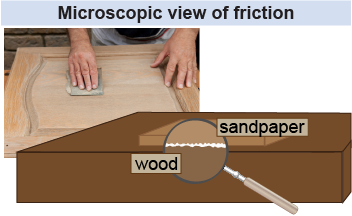There are two broad categories of friction. “Dry” friction is commonly found with materials rubbing against each other, whereas drag (or fluid friction) is the resistance caused by an object moving through, and colliding with, particles in a medium. Viscosity and air resistance are examples of drag. Drag increases with the object’s velocity, whereas dry friction is nearly independent of the object’s velocity.
When two surfaces slide across each other, what causes the friction between them? The amount of friction depends on the set of materials. Imagine dragging a heavy rubber block across a rubber surface, for example, and compare this to the frictional force you would expect if you dragged the same block over ice. The explanation for why a pair of materials has a high or low coefficient of friction lies in their relative tendency to form strong bonds. In spots where the two surfaces actually make contact on the molecular level, “cold welding” occurs. The strength and number of these small bonds depends on the types of materials used. As the surfaces move relative to each other, these bonds are continually broken and reformed. It takes work to overcome the force of these bonds, and heat is generated in the process of breaking these bonds. 
|
|
In problems involving friction, work done against friction is energy that cannot appear in other forms. When you set up the conservation of energy equation, the work done against friction appears in the final state, after the change has occurred.
|
|
Work done against friction converts kinetic energy mostly into heat and wear. Heat is thermal energy that raises the temperature of the system and surroundings. On the microscopic scale, heat is the kinetic energy of atoms and molecules, which you will learn about on page 666 in Chapter 23. Because of entropy, that energy is not recoverable in the sense that it cannot be converted back into kinetic energy. Friction also produces wear, which is the breaking of matter into smaller particles.
|
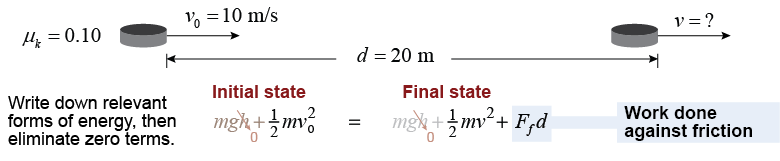For example, a 170 g hockey puck with an initial speed of 10 m/s slides with a coefficient of friction of μk = 0.10. What is its speed after moving 20 m? | Asked: | final speed v | | Given: | coefficient of kinetic friction μk = 0.10, mass of puck m = 0.17 kg,
initial velocity v0 = 10 m/s, distance traveled d = 20 m | | Relationships: | Ff = μkmg, W = Fd, Ek = ½mv2 | | Solution: | |
|
In many circumstances work is done against friction but the net change in kinetic energy is zero! For example, a swimmer expends 2,500 J of energy swimming 25 m across a pool. Friction exerts a force of 100 N against him. - How much work is spent overcoming friction?
- What is the change in the swimmer’s kinetic energy?
| Asked: | (a) the work W done against friction and
(b) the change in kinetic energy ΔE | | Given: | ΔE = 2,500 J, Ff = 100 N, d = 25 m | | Relationships: | W = Fd, ΔE = Qfriction + W | | Solution: | (a) The work done against friction is W = Fd = (100 N)(25 m) = 2,500 J.
(b) The change in energy is ΔE = Q + W = 2,500 J − 2,500 J = 0.
There is no change in kinetic energy since all the work done by the swimmer (2,500 J) is spent overcoming friction. |
|
|
|
Katie pushes on a 10 kg box with 70 N of force, but the box only accelerates by 3 m/s2. How much friction is there? - 0.3 N
- 7 N
- 20 N
- 40 N
 |
If the 10 kg box accelerates by 3 m/s2, the net force is This means that there is a friction force of 40 N to cancel out part of the 70 N applied force. 
|
| |
|
