|
Scientific notation is a way of expressing a number as a coefficient multiplied by a power of 10. This is useful because many values in physics are either too large or too small to write as ordinary decimal numbers. The coefficient is a decimal number, greater than (or equal to) 1 but less than 10. Powers of 10 are 10−1 = 0.1, 100 = 1, 101 = 10, 102 = 100, and so on. For example, the number 1,500 is 1.5×103. The number 1.5 is the coefficient. The number 103 is a power of 10. The small, raised numeral 3 is the exponent. For the number 1,500, this may seem like more trouble than it is worth. But consider a very large number, such as the speed of light, which is 3 hundred million or 300,000,000 m/s. In scientific notation this is 3×108 m/s, which is much easier to write without making a mistake. 
 |
Physics deals with everything from the smallest imaginable to the largest possible. This means working with values that describe objects that are smaller than atoms and with values that describe whole galaxies and the entire universe. As an example, the size of the nucleus of an atom is 0.000000000000001 meters, or 1 × 10-15 m. Our Milky Way Galaxy spins once every 255 million years, or once every 8 trillion seconds (8×1015 s). The average life of a human being is 2.2 billion seconds (2.2×109 s). The time it takes light to get from this page to your eyes is 0.000000002 seconds (2×10–9 s). The usual way we write decimal numbers is impractical for dealing with such a wide a range of values. 
|

|
For numbers less than one, scientific notation uses negative exponents. For example, the number 0.001 is 1 ÷ 1000 = 1 ÷ 103 = 10–3. A negative sign on the exponent of 10 does not mean that the number is negative! In scientific notation, negative exponents mean a value that is less than one. For example, the quantity 0.0025 m is 2.5×10–3 m. 
|
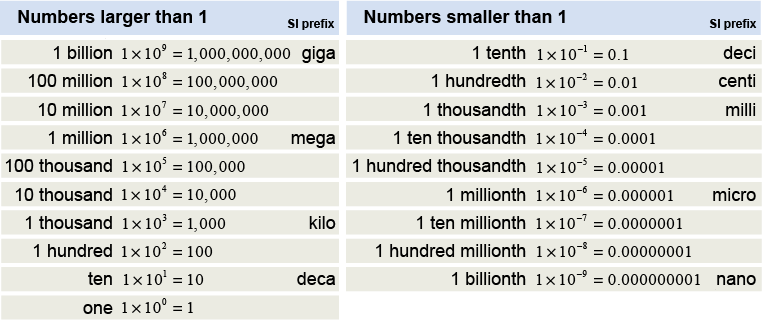
Scientific notation can also be represented by adding a prefix to the quantity. Two thousand meters is the same as 2×103 meters or 2 kilometers, where “kilo” means “one thousand” and is abbreviated “km.” The tables below show some useful prefixes. 
|
|
Computers and scientific calculators use scientific notation. Instead of the multiplication sign (×) a computer uses the letter “E” and a calculator uses either “E” or “EE.” The letter “E” stands for exponential, which is another term for scientific notation. The diagram below shows how to enter scientific notation numbers on a calculator and computer. Pay close attention to the order in which you use the +/− key when you need to enter a negative exponent on a calculator! 
|

|
Which of the following is equal to 32,000,000? - 3.2×10−1 kiloseconds
- 3.2×101 megaseconds
- 3.2 gigaseconds
- 3.2×106 seconds
 |
The correct answer is b, 3.2×101 megaseconds. Mega is 106, so this is equivalent to 3.2×107. 
|
| |
|

