|
Mathematics is the language of physics. Mathematics provides us with a concise and efficient way to describe physical phenomena. Consider speed, which is the distance you traveled divided by the time it takes. For example, if you go 120 miles in 2 hours, your speed is 120 miles ÷ 2 hours, or 60 miles per hour. If we write this in algebra, we let the variable v stand for “the speed,” d stand for “the distance you go,” and t stand for “the time it takes.” The sentence that defines speed translates to an equation that says the same thing. 
 |
Every piece of information in a physics problem must have a name to appear in an equation. - For most problems the first letter of the word is the variable name. For example, d is distance and m is mass.
- When there are two different masses, we use subscripts to tell them apart. For example, m1 (or “m sub one”) is the first mass and m2 is the second mass.
- For initial values, such as the height at the start of a problem, the subscript 0 (zero) is used. For example, the initial height would be h0 (or “h sub zero”).
- There are certain quantities for which specific letters are used that are different from the first letter of the word. For example, the variable v is used to represent speed because it is the first letter in velocity.

|

|
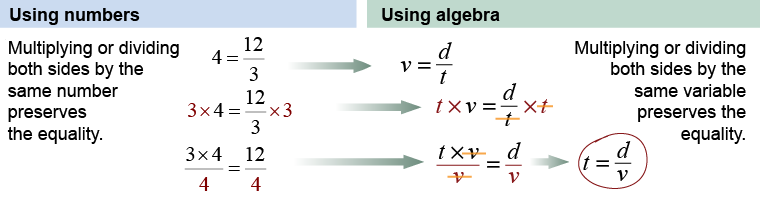
The language of mathematics provides techniques for rearranging variables while preserving the relationship among them. As an example, try to rearrange the sentence defining speed in a way that says “the time taken is equal to....” The correct answer is that the time taken is equal to the distance traveled divided by the speed. If you have to travel 120 miles and your speed is 60 mph, it takes you 2 hours because 2 hr = 120 mi ÷ 60 mph. There is no way to know how to rearrange an English sentence that will provide this result. But there is a way to do it with algebra. 
|
|
The key to using algebra is understanding the equals (=) sign. It means that whatever is on the left of the equals sign is the same as what is on the right. It also means that if you add something to the left, you have to add the same something to the right to preserve the equality. Learning what to add, subtract, multiply, or divide on both sides of the equation allows you to rearrange equations to turn the relationship you have into the one you want. The diagram illustrates how this works to solve the speed equation for time. 
|

|
Solve the equation v = d/t for d. - d = tv
- d = 1/tv
- d = t/v
- d = v/t
 |
The correct answer is a, d = tv. 
|
| |
|

