|
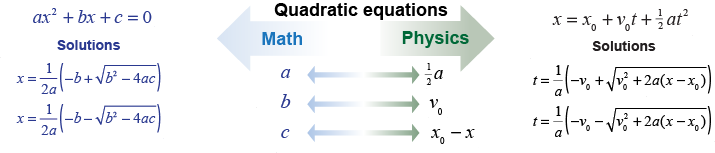
Notice that the position equation has terms involving time and also time squared. Equations that involve a variable squared are called quadratic equations. An equation is said to be quadratic in x if x2 appears as the highest power of x in the equation. Quadratic equations are special for two reasons: - There are special techniques for solving them.
- There are two solutions for the squared variable.

|
|
The variables c, b, and a in the math formula are the coefficients of x0 (= 1), x1 = x, and x2.The two solutions are true for any values of the variables. In physics, we will sometimes need the quadratic solutions above; but in some cases we can also use the easier method of factoring a quadratic equation to solve for the two solutions. 
|

|
To find the solution we start as usual by defining the initial position as x0 = 0. We are also given that the arrow comes back down to x0 = 0 again 5.0 s after it is fired upward. The position equation becomes a quadratic in time t, from which a t can be factored from each term to give this intermediate equation: |
There are two ways in which the result can be zero: |
The solution on the right gives us what we want, which is the value of v0 when t = 5.0 s. The solution on the left is also realistic since it says the arrow was on the ground (x = 0) at the start when t = 0. 
|
| |
|

