|
The concept of acceleration is not easy to understand. It took Newton’s genius and the invention of a whole new form of mathematics (calculus) to fully define acceleration. Acceleration is important enough to understanding forces and motion that it is worth learning about it more deeply by discussing it with teachers and peers. 
|
|
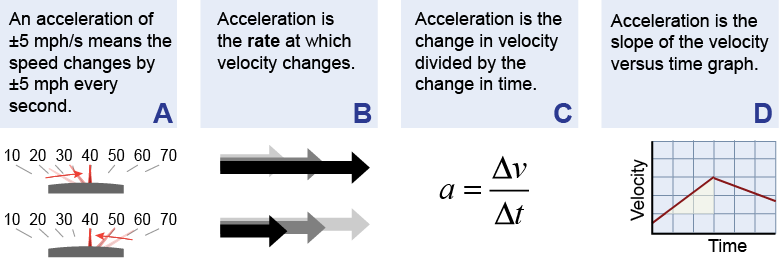
The diagrams below illustrate the concept of acceleration. Display these diagrams on a projector and discuss statements A–D that accompany each diagram. Use the questions below to focus the discussion in groups and with the teacher.
|
|
- How does statement A relate to the diagram below it?
What does “+/− 5 mph/s” mean? - What does the word “rate” mean in the context of statement B? How do the arrows below represent the idea of a rate of change of velocity?
- How does the equation represent statement C? Answer by translating each symbol and operation. For example the horizontal line means “divided by.” Give numerical examples of a change in velocity divided by a change in time.
- How does the diagram in D represent the text of statement D? What does the shaded triangle represent? What does it mean that the lines on the velocity versus time graph in diagram D go up, then down? How is that reflected in the concept of acceleration?
|
Describe a personal experience that relates to diagram A using the word “acceleration.” Your story should include both the upper and lower parts of the diagram. The following story provides an example.
“If I push down on the gas pedal on a level road the car accelerates by about five miles per hour every second. From a stop it takes 12 s to get to 60 mph. If I hit the brakes gently, I can decrease the speed back to zero over 12 s, for an acceleration of −5 miles per hour per second.”
|
