|
The equation defining acceleration can be rewritten as a model that describes how the velocity changes over time. The result is equation (4.2), which gives the instantaneous velocity v at time t under the assumption that the acceleration a is constant. 
 |
In equation (4.2), we are not using the notation Δt = tf − ti. Instead, time t is used as a continuously variable quantity. When we make this change for time t, the way we write the velocity also changes. In equation (4.2) we are creating a model for the velocity that can be used for any time t. So we use the notation that v0 is the velocity when time is t = 0, but we use v to represent the velocity at any time. Many people will use the notation v(t) to represent explicitly how velocity is a function of time.
An alternate way to express equation (4.2) for two particular points in time is | |
This equation, however, represents the velocity at two particular times and is not a model for the velocity. 
|
| (4.2) | | | v | = | velocity (m/s) | | v0 | = | initial velocity (m/s) | | a | = | acceleration (m/s2) | | t | = | time (s) |
| Velocity
for constant acceleration |
|
|
In this equation we set Δt = t by assuming the motion starts at t = 0. The initial velocity v0 is the velocity when t = 0.
|
The velocity model in equation (4.2) corresponds to the equation of a straight line when plotting velocity versus time. In recognizing this comparison between the mathematics of a straight line and the velocity in accelerated motion, don’t be tricked because the right-hand side of equation (4.2) has the position of the terms at and v0 switched! The slope of the line—the coefficient in front of time t—is the acceleration a. The intercept on the vertical axis—the constant value added to the equation—is the initial velocity v0.
|
|
A cart traveling at 1 m/s reaches a hill and accelerates down the hill at 0.5 m/s2. What is the velocity of the cart 3 s after it starts accelerating?
|
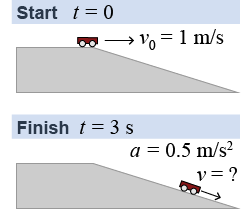
| Asked: | instantaneous velocity v | | Given: | initial velocity of v0 = 1 m/s, acceleration a = 0.5 m/s2, and time t = 3.0 s | | Relationships: | v = v0 + at | | Solution: | | v | = | 1 m/s + (0.5 m/s2)(3.0 s) | | | = | 2.5 m/s | |
|
|
In the above example the velocity and acceleration are in the same direction—both are positive. The speed increases from 1 to 2.5 m/s. Acceleration can also decrease an object’s speed when the sign of the velocity is different from the sign of the acceleration. For example, an acceleration of −1 m/s2 adds −1 m/s to the velocity each second. This would decrease a positive velocity. It would also make a negative velocity more negative—that is, faster in the negative direction.
|
|
A cart traveling at 2 m/s along a level surface reaches an upward sloping hill and accelerates at −0.5 m/s2. What is the velocity of the cart 3 s after it starts climbing the hill?
|
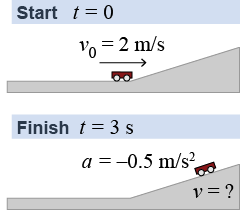
| Asked: | instantaneous velocity v | | Given: | initial velocity of v0 = 2 m/s, acceleration of a = −0.5 m/s2, and time of t = 3 s | | Relationships: | v = v0 + at | | Solution: | | v | = | 2 m/s + (−0.5 m/s2)(3.0 s) | | | = | 0.5 m/s | |
|
|
The model of motion given by equation (4.2) applies to the instantaneous velocity at time t. Translated to an English sentence the equation tells us that the velocity v at time t is the initial velocity v0 plus the change in velocity due to acceleration a applied every second for t seconds. The assumption of constant acceleration means that the change in velocity each second is the same.
|
Can you describe a situation in which an object’s acceleration is negative but its speed is increasing?
 |
If the velocity is negative, then a negative acceleration makes the velocity more negative every second. This increases the speed since speed is the absolute value of velocity. For example, suppose the velocity starts at −10 m/s and the acceleration is −1 m/s2. After one second the velocity is −11 m/s. After two seconds the velocity is −12 m/s. The speed increases from 10 to 12 m/s. 
|
