|
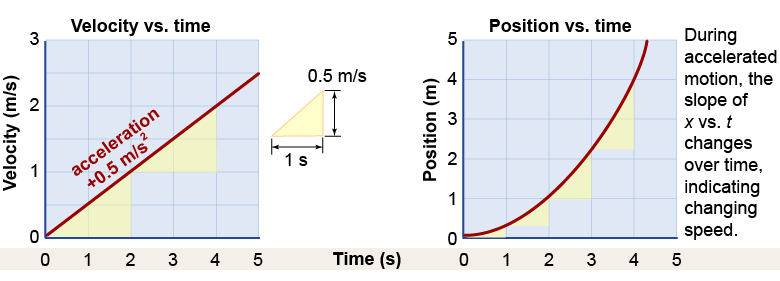
A moving object with an increasing velocity covers more distance during each new second than it covered in the previous second. That means the slope of the x vs. t graph must become steeper over time as the velocity increases. The changing slope is what we recognize as a curve.
In general, acceleration results in curves on the x vs. t graph. 
|
Accelerated motion looks different on the v vs. t and x vs. t graphs. Constant acceleration means that the velocity changes by the same amount every second—which produces a straight line of constant slope on a v vs. t graph but results in a curved line on the x vs. t graph. 
|
|
The acceleration equals the slope of the velocity versus time graph. In the example above, the velocity increases by 0.5 m/s in 1 s. This is equal to an acceleration of 0.5 meters per second per second or 0.5 m/s2. A positive slope on a v vs. t graph means positive acceleration. A negative slope on a v vs. t graph means negative acceleration. Do not confuse the sign of the slope of the v vs. t graph with the sign of the velocity itself! You can have negative acceleration with positive velocity and vice versa. 
|
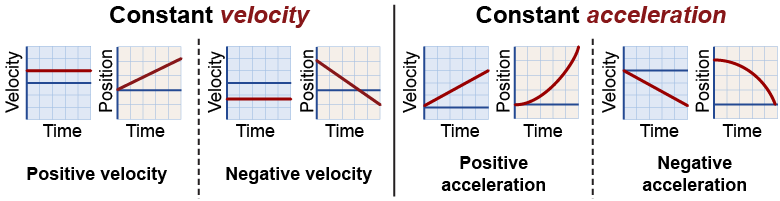
Constant velocity, or constant speed, both mean that the acceleration is zero. The position changes by the same amount in equal time intervals and the result is a flat v vs. t graph and a constant-slope x vs. t graph. Constant acceleration means that the velocity changes by an equal amount in equal time intervals. This means a constant-slope v vs. t graph and a curved x vs. t graph. 
|
|
Graphical models for motion with constant acceleration are illustrated above and compared to graphical models for motion with constant velocity. You can quickly scan the shapes of these graphs and identify which kind of motion is being modeled in each case. 
|
Constant positive acceleration looks like which of the following on a velocity versus time graph? - linear positive slope
- curved positive slope
- linear negative slope
- curved negative slope
|

