|
The acceleration of a moving object depends on two factors: - the amount the object’s speed changes (Δv) and
- the time over which the change occurs (Δt).
Unless it is otherwise stated, you should assume that the acceleration in a physics problem is constant. Thus the speed changes by the same amount every second. 
|
What is the acceleration of a cart that rolls down a hill if it starts at rest and reaches a speed of 1.2 m/s after 0.6 s?
| Asked: | acceleration a | | Given: | change in speed of Δv = 1.2 m/s, interval of time Δt = 0.6 s | | Relationships: | a = Δv/Δt | | Solution: | a = 1.2 m/s ÷ 0.6 s = 2 m/s2 |
|
Another type of problem asks for the speed of an object given the acceleration and time. The change in speed Δv for an accelerated object is What is the speed of an object that starts from rest and accelerates at a constant 2 m/s2 for 10 s? | Asked: | final speed v | | Given: | acceleration a = 2 m/s2, time interval of Δt = 10 s,
and initial speed v0 = 0 (from rest) | | Relationships: | a = Δv/Δt → Δv = aΔt | | Solution: | We use the change in speed Δv = v − v0 to rewrite the equation as v − v0 = aΔt → v = v0 + aΔt Then we calculate the final speed v = 0 + (2 m/s2 × 10 s) = 20 m/s |
|
|
|
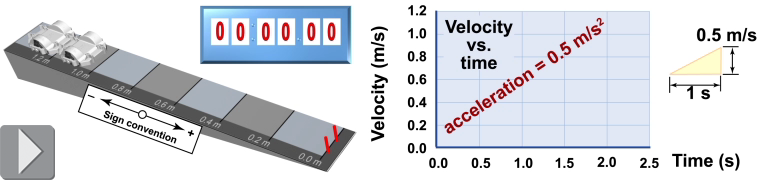
Acceleration causes a nonzero slope on the velocity versus time graph, because acceleration represents change in velocity over time. Mathematically, the slope of a v vs. t graph is the change in velocity divided by the change in time, which is the definition of acceleration. In the example above, velocity increases at a steady rate of 0.5 m/s each second, producing a straight-line graph with a slope of 0.5 m/s2.
|
