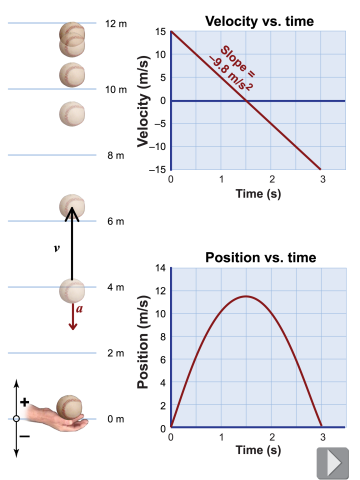|
A ball thrown upward eventually comes back down again. The model for accelerated motion in equations (4.2) and (4.3) allows us to determine position (height) or velocity at all points in the motion:
| (4.2) | v = v0 + at | | (4.3) | x = x0 + v0t + ½at2 |
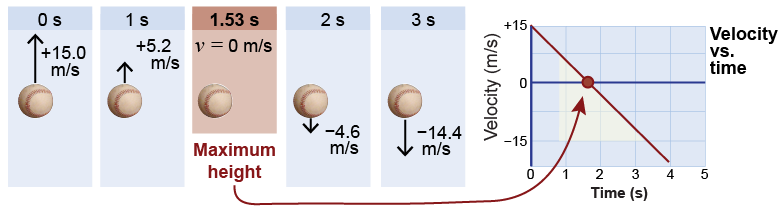
As an example, consider throwing a baseball straight up with a velocity of +15 m/s. The acceleration of gravity is −9.8 m/s2, and so the ball’s velocity changes by −9.8 m/s every second. After 1 s, the ball has a speed of only 5.2 m/s and by 2 s its velocity has reversed direction and the ball is heading downward at −4.6 m/s. 
|
|
|
A common problem asks for the highest point reached when an object is thrown vertically upward. This problem is solved by recognizing that the vertical velocity is zero at the highest point. If the vertical velocity were not zero, then the object would continue to move upward. The velocity equation tells you the time it takes to reach a velocity of zero, while the position equation tells you the height the object reaches at that time.
|
| Asked: | height, which is the final position x | | Given: | initial velocity of 15 m/s, acceleration of −9.8 m/s2 | | Relationships: | v = v0 + gt
x = x0 + v0t + ½gt2 | | Solution: | v = v0 + at → t = v0/g = 15 m/s ÷ 9.8 m/s2 = 1.53 s | x = x0 + v0t + ½gt2 → x | = | (15 m/s)(1.53 s) − ½(9.8 m/s2)(1.53 s)2 | | | = | 11.5 m | |
|
|
Look more carefully at the illustration at the top of the page. The position of the baseball is plotted repeatedly every 0.25 s. This particle model of motion shows you that the speed was slowest at the top because successive ball images are close to each other. Objects are often replaced by small dots when creating a particle model.
|
