Solving problems with the four equations
Four equations for solving motion problems
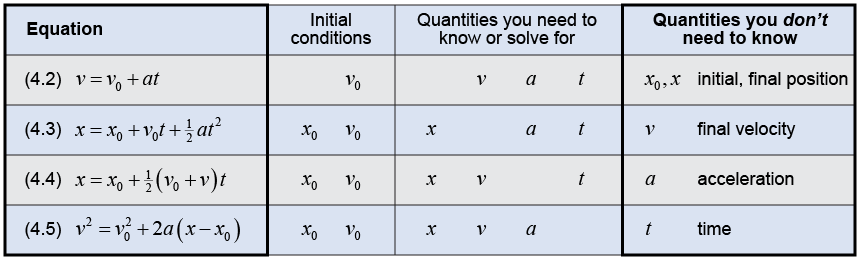
Understanding the four equations Equations (4.2), (4.3), (4.4), and (4.5) are useful for solving a wide variety of problems in physics. Each equation is a little bit different in terms of which quantities it uses—and which quantity it omits. Examine the table above to see how the first equation does not include a variable for position (either x or x0), the second equation does not include final velocity v, the third equation does not include acceleration a, and the fourth equation does not use time t.
Which equation should I use? Most motion problems have one quantity that you don’t need to know.
  1. Write down the given quantities in the problem.
  2. Write down the quantity for which you are asked to solve.
  3. Determine which quantity you don’t need to know.
  4. Choose the equation based on #3.
Determine the stopping time A car is moving at 20 m/s when the driver brakes and comes to a stop after traveling 30 m. If the car’s deceleration were constant, how long did it take for the car to stop?
Asked: time t
Given: initial velocity of v0 = 20 m/s, final velocity v = 0 m/s (comes to a stop),
and displacement x − x0 = 30 m
Relationships: The acceleration is neither given nor asked for, so use x− x 0 = 1 2 ( v 0 +v )t
Solution: Solve the equation for time: t=2( x− x 0 v 0 +v )=2( 30 m 20 m/s+0 m/s )=3 s
Highway on-ramp problem A car needs to accelerate from a standstill along a 150 m long on-ramp to merge into traffic moving at 25 m/s. What is the car’s acceleration?
Asked: acceleration a
Given: initial velocity of v0 = 0 m/s (standstill), final velocity v = 25 m/s,
and displacement x − x0 = 150 m
Relationships: The time is neither given nor asked for, so use v 2 = v 0 2 +2a( x− x 0 )
Solution: Solve the equation for acceleration: a= v 2 − v 0 2 2( x− x 0 ) = ( 25 m/s ) 2 − ( 0 m/s ) 2 2( 150 m ) =2.1  m/s 2
Previous Page Next Page117