|
You can ride a bicycle fast on hard pavement, but when you switch surfaces to sand, gravel, or mud you must slow down. Your speed on a bicycle depends on the medium you are traveling on. In the same way, the observed speed of light depends on the properties of the medium in which the light travels. 
 |
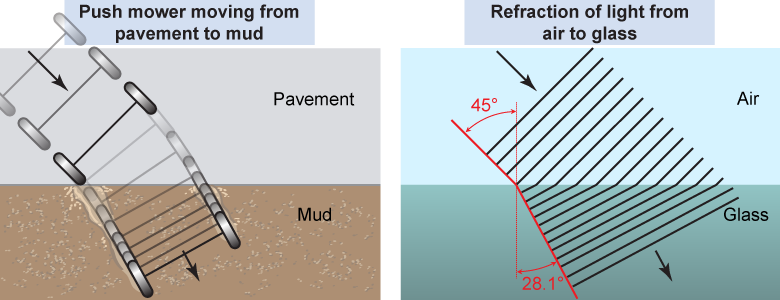
Imagine a push mower moving at an angle when it goes from pavement to mud. The wheel that first enters the mud will slow down. The other wheel will spin toward the boundary, because it still can move faster on the pavement. The mower turns a bit as it moves from one medium to the other. In the same way, a light wave propagates more slowly in glass than in air. The difference in propagation rate is the explanation for refraction as the wavefronts are slightly retarded in the low-index (low-n) medium compared to the higher n medium. 
|
|
The physical phenomenon of refraction—where light bends as it propagates from one medium to another—is a consequence of the change in the speed of light between those two media. The index of refraction for a medium, such as glass or water, represents how the speed of light has changed relative to a vacuum and is described by equation (22.2). 
|
| (22.2) | | | n | = | index of refraction | | c | = | speed of light in a vacuum (m/s) | | v | = | speed of light in medium (m/s) |
| Index of refraction
|
|
When the speed of light v changes as it moves from one medium to another, how are the frequency f and/or wavelength λ affected? Frequency cannot change at the boundary between the two materials, because the number of waves per second that arrive and depart there must be equal. Instead, the wavelength of light changes from one medium to another to match the changes in the speed of light through the equation v = fλ. Look again at the illustration above: Notice how the spacing between waves is smaller in glass than in air. The wavelength of light is shorter in glass than in air in the same way that the speed of light is lower in glass than in air. 
 |
As we will learn in a few pages, the energy of light is related to its frequency according to the Planck equation E = hf. When light propagates from one medium to another, its energy is conserved. Refraction redirects light, rather than absorbing light. If energy E stays the same when light is refracted, then frequency f must also stay the same. 
|
What is the speed of light through saltwater if its index of refraction is 1.34? | Asked: | speed of light v in saltwater | | Given: | index of refraction of saltwater, nw = 1.34;
speed of light in air (nearly same as a vacuum), c = 3.0×108 m/s | | Relationships: | index of refraction for water, nw = c/v | | Solution: | Solve for the speed of light in water by multiplying by v: then dividing by nw: | | Answer: | v = 2.2 × 108 m/s | 
|
When traveling through diamond, light travels at approximately 1.25 × 108 m/s. What is diamond’s index of refraction? - 0.42
- 1
- 1.75
- 2.4
 |
The correct answer is d. The relevant formula here is n = c/v. 
|
What is the index of refraction for a vacuum? - 0
- 1
- 3×108
- 3.14159
 |
The correct answer is b. The index of refraction is the ratio of the speed of light in a vacuum to its speed in a given medium. Because the medium is a vacuum, the index of refraction is 1. 
|
Estimate the value for the index of refraction for air (na). - na < 0
- 0 < na < 1
- 1 < na < 1.33
- 1.33 < na
 |
The correct answer is c. Light in air moves slightly slower than light in a vacuum, as it is impeded by molecules, but does not move as slowly as it does in water or glass. In reality, the speed of light in air is close to the speed of light in a vacuum. The index of refraction for air is 1.0003 but is usually treated as 1.00. 
|
Why are none of the indices of refraction less than 1?
 |
An index of refraction for a material is the ratio of the speed of light in a vacuum to its speed in the material. The maximum speed that light (or anything) can travel is the speed of light in a vacuum. Because nothing can go faster than that, there cannot be an index of refraction of less than one. 
|

