|
 While bringing a world of news and entertainment to millions, AM radio and similar technologies have limitations: Interference can add an annoying hiss and reception quality can vary. Today’s technology, however, allows us to reliably digitize, store, and exchange nearly perfect copies of speech, music, and even high-definition video with people across the globe. Many forms of modern communication use infrared (IR) and visible light, which are EM waves that vibrate much more rapidly than radio waves. With frequencies of many trillions of hertz (terahertz, or THz), such waves can easily convey billions of bytes (or gigabytes) of data each second—making it possible to create the impression of smooth, realistic motion across a large screen.
While bringing a world of news and entertainment to millions, AM radio and similar technologies have limitations: Interference can add an annoying hiss and reception quality can vary. Today’s technology, however, allows us to reliably digitize, store, and exchange nearly perfect copies of speech, music, and even high-definition video with people across the globe. Many forms of modern communication use infrared (IR) and visible light, which are EM waves that vibrate much more rapidly than radio waves. With frequencies of many trillions of hertz (terahertz, or THz), such waves can easily convey billions of bytes (or gigabytes) of data each second—making it possible to create the impression of smooth, realistic motion across a large screen. 
|
Whereas radio transmissions are usually described as waves, visible and infrared forms of light are best thought of as particles, since their wavelengths are microscopically small. (The near-infrared photons most commonly used in telecommunications have wavelengths of 1,550 nm or 1.55×10−6 m, roughly 1/100th the width of a human hair.) Furthermore, visible and IR radiation usually are detected by devices that rely on the photoelectric effect, which you read about on page 650. When a near-infrared or visible photon smacks into such a device, it knocks an electron loose, thereby creating electric current. This collision can most easily be understood by thinking about the light as a stream of individual photons. 
|

|
Visible and near-infrared light can’t wiggle through clouds and fog the way radio waves can. Yet such light has fantastically high frequencies and information-packing power. How can we use light to transmit data from city to city and country to country? By guiding it from place to place along as smooth a road as possible. And that road is a bundle of optical fibers, which are spaghetti-like strands of glass. (Optical fibers are so ubiquitous that you can now find them in novelty stores.) Light enters an optical fiber much like it enters the lens in your eye: by refraction from air into the fiber material. Once inside, the light is prevented from escaping from the fiber by a series of total internal reflections, until it reaches the far end of the fiber. The internal reflections off the inside surface of the fiber can only happen if the light enters the fiber at a suitably small angle of incidence! 
 |
 Optical fibers have two basic elements, both made of very pure glass: a core through which the light signal travels, and cladding engineered to trap the light within the core. The cladding is designed to have a lower index of refraction than the core. This enables total internal reflection to operate on suitably angled light rays.
Optical fibers have two basic elements, both made of very pure glass: a core through which the light signal travels, and cladding engineered to trap the light within the core. The cladding is designed to have a lower index of refraction than the core. This enables total internal reflection to operate on suitably angled light rays.
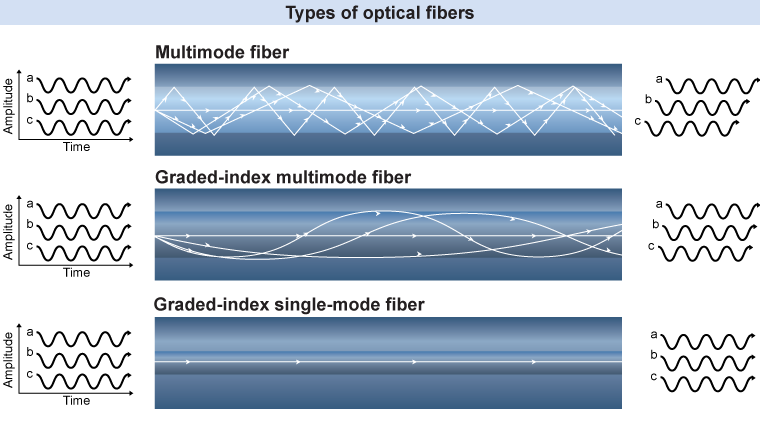
Simple multimode fibers can capture lots of light, and they are relatively easy to make. Unfortunately, they allow different light rays to travel different distances from end to end, since the rays bounce off the core walls at differing angles. Since all of those rays travel at the same speed (being the same color), the rays will emerge at slightly different times, even if they entered together. That effect limits how many bytes of data can be transmitted each second.
Graded-index multimode fibers are engineered so that the index of refraction varies smoothly from the center of the core to its edge. Such fibers keep the photons in a single light pulse from spreading out too much. An extreme version, the graded-index single-mode fiber, has a very narrow core, measuring only a few wavelengths of light in diameter. Best used with lasers, it allows light pulses to travel dozens of kilometers while hardly spreading out at all. Fiber optics are so important to today’s technologies that engineer Charles Kao, a pioneer in the field, shared in the 2009 Nobel Prize in Physics. 
|
Most long-haul optical-fiber networks rely on near-infrared light with a wavelength of 1,550 nm, or 1.55×10−6 m. This light travels at a speed of 2.04×108 m/s in the fiber’s core. What is the core’s index of refraction for this particular type of light? - 1.3×1014
- 316
- 1.47
- 0.68
 |
The correct answer is c.
Asked: index of refraction, n, for light in optical fiber core
Given: speed in fiber, v = 2.04×108 m/s
Relationships: n = c⁄v; speed of light, c = 3×108 m/s
Solve: 
|
Near-infrared light has a much shorter wavelength than radio waves. Which of the following must be true? - Near-infrared light travels slower than radio waves in a vacuum.
- Near-infrared light travels faster than radio waves in a vacuum.
- Near-infrared light has a lower frequency than radio waves.
- Near-infrared light has a higher frequency than radio waves.
 |
The correct answer is d. Frequency and wavelength are inversely related by the equation c = fλ.
Answers a and b are incorrect, because all electromagnetic waves (whether radio or infrared) travel at the same speed in a vacuum. 
|
| |
|

