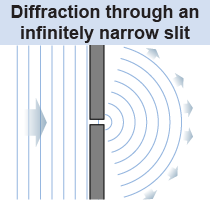|
If light diffracts around an object, does it also diffract through a narrow opening? In Chapter 15, you learned that waves diffract through a narrow slit with a pattern similar to that shown in the illustration at right. As long as the slit or opening is very narrow compared to the wavelength of the waves, then the diffracted waves form nearly circular arcs. Does light behave in the same way? 
|
|
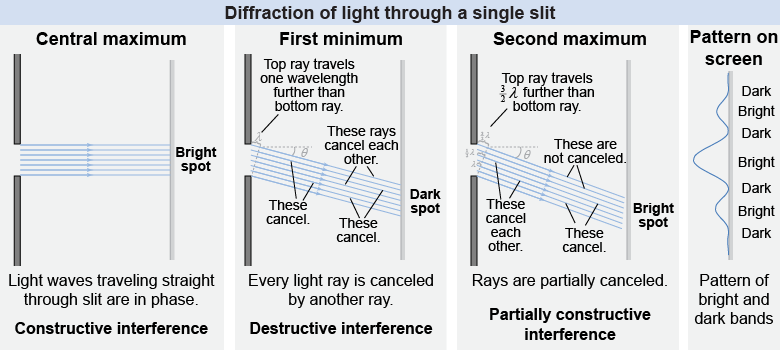
The diffraction pattern shown above represents diffraction through a slit of infinitely small width. How many real slits are that narrow? None! In real physics situations, the slit has a measurable width, which leads to a more complicated diffraction pattern. The reason for this pattern is that light through one side of the slit can interfere with light passing through the other side of the slit.
|
|
|
The illustration above shows light passing through a realistic slit and the diffraction pattern produced on a screen behind the slit. Light passing straight through the slit adds constructively to create a bright, central spot on the screen.
|
|
At larger projection angles θ onto the screen, light from different parts of the slit travels different distances to reach the screen. A ray from the top of the slit has to travel one-half a wavelength further than a ray from the middle of the slit, resulting in destructive interference. In fact, every ray through the slit at that angle will be canceled by another ray! This causes a dark spot on the screen at that location.
|
|
At a larger angle, light from one side of the slit will travel (3/2)λ further than light from the other side. At this angle, some of the light interferes destructively, while one-third of the light interferes constructively, leading to a bright spot on the screen.
|
This pattern of bright and dark spots repeats at larger angles, although the brightness of the spots gets fainter. This diffraction pattern shows that light is interfering with itself, which means that light is exhibiting wave behavior.
 |
Where do the maxima and minima occur when light through a slit is diffracted onto a screen? There is a central maximum on the screen, where the projection angle (or its deviation) is θ = 0°. The other maxima and minima are given by | | | D | = | slit width (m) | | θ | = | projection angle (degrees) | | λ | = | wavelength of light (m) | | m | = | order (1, 2, 3, ...) |
| Single slit diffraction
minima |
| | | D | = | slit width (m) | | θ | = | projection angle (degrees) | | λ | = | wavelength of light (m) | | m | = | order (1, 2, 3, ...) |
| Single slit diffraction
maxima |
|
