|
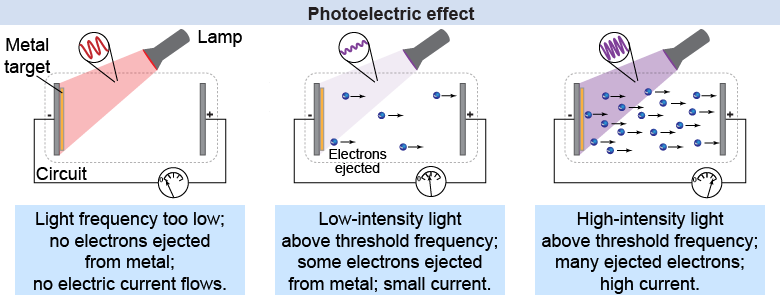
Hertz in 1887 discovered that an ultraviolet light source shining on a metal’s surface would increase electrical sparks—later recognized to be electrons ejected from the metal—across the gap between two metal plates. The photoelectric effect occurs when electrons are ejected by illuminating a metal surface with light. 
|
|
Subsequent researchers showed several curious results. Lower frequency light, such as red light, never liberated electrons no matter how bright the light source. Higher frequency light, such as ultraviolet light, would always eject electrons no matter how faint the light source—although the number of electrons varied with the intensity of the light. In classical physics it was assumed that light was an electromagnetic wave, which meant that the energy of the ejected electrons should be a function of the intensity and frequency of the light, not just frequency. What was wrong with this picture? 
 |
There was another property of the photoelectric that was difficult to explain with the wave model for light from classical physics. In the wave model, low-intensity light would take some time to deposit enough energy to cause the electrons to vibrate sufficiently to break free from their atoms. But the observational results showed that electrons were immediately released, no matter how faint the incident light. This lack of a delay time for low-intensity light confounded the classical physicists! 
|
Albert Einstein in 1905 explained the photoelectric effect with two insights. First, he assumed that light was composed of quantized photons, each with its own, indivisible bundle of energy. Second, the atoms in the metal held onto their electrons with a binding energy called the work function. Only if the photon’s energy was high enough to exceed the work function would an electron be ejected. Since Planck had already proposed a photon’s energy to be related to its frequency, the minimum energy of the work function corresponded to a threshold frequency for electrons to be ejected. 
|
How much energy do the ejected electrons have? Part of the energy of the incident photon liberates the electron from the metal; the remainder of the photon’s energy is converted into kinetic energy of the electron. The photon energy required to liberate the electron is called the work function. The kinetic energy of the electron is therefore the difference between the incident photon energy and the work function of the metal, as given by equation (22.4). The work function is a property of the metal; different metals have different values for their work function. 
|
| (22.4) | | | Ek | = | maximum energy of ejected electron (J) | | h | = | Planck’s constant = 6.63×10−34 J s | | f | = | frequency of incident light (Hz) | | W0 | = | work function for metal (J) |
| Photoelectric
effect
|
|
The value for the work function of a material is usually very small, on the order of 10−19 J. Because of this, it is convenient to use a different unit of energy to express the work function. The electron volt is a unit of energy that is used to express changes in energy on an atomic scale. One electron volt is equal to 1.602×10−19 J. 
|
Why won’t even very bright, low-frequency light cause electrons to be ejected from metal via the photoelectric effect?
 |
The brightness (intensity) of the light depends only on how many photons are in it. Even though there are many photons hitting the metal when the light is bright, none of these photons have enough energy in themselves to knock any electrons free. 
|

