|
If you shine light at a small object, such as the paper clip in the figure at right, you’ll see something peculiar: a series of bright and dark rings (or bands) surrounding the shadow of the object! This diffraction pattern of bright and dark bands is caused by constructive and destructive interference when light passes around a barrier or through an opening. 
|
|
How do diffraction and interference create this pattern? On page 422, you learned how waves diffract around the edge of an obstacle. Sound waves can diffract around the wall of a room, but light waves cannot, because the wavelength of light is much smaller than the size of the barrier. What happens if you use a smaller barrier, such as a paper clip? Does light diffract around it?
|
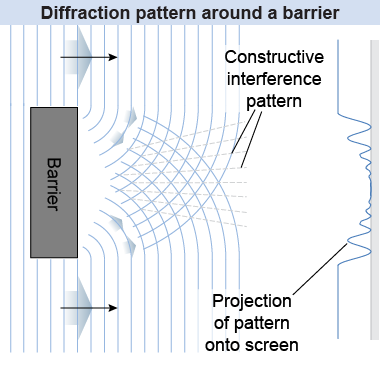When light waves pass a barrier, a little bit of the light’s intensity diffracts around the barrier’s corner. These waves can interfere with light waves diffracting around the other side of the barrier, which creates a pattern of interference. If the diffracted light is projected onto a screen, such as in the illustration at the top of this page, you will see a pattern of bright and dark bands around the edge of the barrier. The bright bands are constructive interference, whereas the dark bands are destructive interference. The brightness of the interference bands falls off away from the edge of the barrier.
 |
Most telescopes are constructed by using circular optics, such as a round lens for smaller telescopes or a round mirror for larger ones. The circular aperture of telescopes has its own diffraction pattern that limits the ability of the telescope to resolve small objects in the sky. The Rayleigh criterion, named after the English physicist Lord Rayleigh (John Strutt, the third Baron Rayleigh), represents the smallest angle θ that can be resolved for a telescope of diameter D that is observing light with wavelength λ: | | | θ | = | smallest resolution angle (radians) | | λ | = | wavelength (m) | | D | = | diameter of telescope (m) |
| Rayleigh criterion
|
Note that the angle in this equation is represented in radians, not degrees!
This smallest angle that can be resolved is called the diffraction limit of the telescope. It represents, for example, the smallest separation of a binary star that can be detected; if the two stars are separated by a smaller angle, they will be blurred together and indistinguishable.
A telescope with a diameter of 10 cm that is making observations in green light (λ = 550 nm) has a diffraction limit of 1.4 arcseconds (where 3,600 arcseconds = 1°). The largest telescopes on Earth, the two 10.4 m Keck telescopes, have a diffraction limit of 0.013 arcseconds. For telescopes at the best mountain sites, however, Earth’s atmosphere blurs the images to 0.5 arcseconds, which limits the resolution of even the largest telescopes. That is why telescopes, such as the Hubble Space Telescope, have been put into orbit: to exploit the diffraction-limited resolution of the telescope without being compromised by blurring by the Earth’s atmosphere. 
|
|
The illustration at the top of this page shows this diffraction pattern for light passing around a paper clip. The diffraction pattern of light is an example of how light can behave like a wave.
|
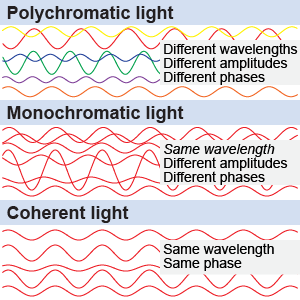The diffraction pattern is difficult to see when you use ordinary, white light. Diffraction is a wave phenomenon, so it is best demonstrated when all the light has the same wavelength. Light waves are called monochromatic if they have the same wavelength, although they may differ in amplitude or phase. Consider the green light color of the illustration at the top of the page. A monochromatic, green light source was used to create it. Furthermore, the light must be coherent or in phase to see the interference pattern from diffraction around a barrier. Lasers are often used as sources of coherent light.
|
| |
|
