Essential Physics

Elastic collisions

In an elastic collision, kinetic energy is conserved as well as momentum. An example of a perfectly elastic collision occurs when an ideal (frictionless) rubber ball bounces off a floor and reaches the same height from which it was initially dropped. A nearly-elastic collision occurs in billiards when a fast-moving cue ball strikes another ball, causing the cue ball to stop in place and the target ball to move off in the same direction. Real collisions are rarely perfectly elastic however, the amount of kinetic energy lost may be so small that it is often a good approximation to assume perfect elasticity. Read the text aloud

Read the text aloud

(11.4)

\frac{1}{2} m_{1} v_{_{i 1}}^{2} + \frac{1}{2} m_{2} v_{_{i 2}}^{2} = \frac{1}{2} m_{1} v_{_{f 1}}^{2} + \frac{1}{2} m_{2} v_{_{f 2}}^{2}

Conservation of energy
for elastic collisions

Elastic collision problems typically involve two equations: conservation of momentum and conservation of kinetic energy. The momentum equation involves the masses and velocities before and after the collision. The energy equation involves the masses and the velocities squared before and after the collision. The squared velocities make the algebra of solving momentum problems a little more challenging. In problems involving two and three dimensions, momentum must be conserved separately in each direction. Kinetic energy is a scalar however, and there is typically only one kinetic energy equation. Read the text aloud

Read the text aloud

Show Quadratic solution to elastic collision problems

What can make an elastic collision problem even more difficult is that the conservation of kinetic energy equation is quadratic in speed; i.e., the speed variables are all squared. In algebra class you learned that if you have a quadratic equation of the form

y = a x^{2} + b x + c

then the two solutions (or roots) of the equation are

x = \frac{- b \pm \sqrt{b^{2} - 4 a c}}{2 a}

More difficult elastic collision problems involving these quadratic equations will be covered in more depth in later chapters in the book. Hide me!

Hide me!

Is this collision elastic?

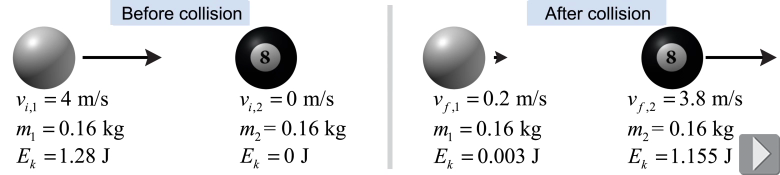A 0.16 kg cue ball traveling at 4 m/s strikes a stationary 0.16 kg eight ball. After the collision, the cue ball travels at 0.2 m/s while the eight ball travels at 3.8 m/s. Is this an elastic collision? Why or why not?

Asked:

whether it is an elastic collision; i.e., is kinetic energy conserved?

Given:

masses of the balls, m₁ = m₂ = 0.16 kg; initial speed v_i1 = 4 m/s of the cue ball; initial speed v_i2 = 0 m/s of the eight-ball; final speed v_f1 = 0.2 m/s of the cue ball; final speed v_f1 = 3.8 m/s of the eight ball

Relationships:

conservation of energy for two objects in an elastic collision:

\frac{1}{2} m_{1} v_{_{i 1}}^{2} + \frac{1}{2} m_{2} v_{_{i 2}}^{2} = \frac{1}{2} m_{1} v_{_{f 1}}^{2} + \frac{1}{2} m_{2} v_{_{f 2}}^{2}

Solution:

Compare the kinetic energies of the balls before and after the collision:

\begin{matrix} \frac{1}{2} (0.16 kg) {(4 m/s)}^{2} + \frac{1}{2} (0.16 kg) {(0)}^{2} & \overset{?}{=} & \frac{1}{2} (0.16 kg) {(0.2 m/s)}^{2} + \frac{1}{2} (0.16 kg) {(3.8 m/s)}^{2} \\ 1.28 J + 0 J & \neq & 0 .003 J + 1.155 J \end{matrix}

Answer:

The collision is not elastic because some kinetic energy is lost. (Since only a small amount of the kinetic energy is lost, the collision is “nearly elastic.”)

Read the text aloud

In elastic collisions, which of the following quantities are conserved?

velocity
momentum
kinetic energy

I only
I and III only
II and III only
I, II, and III

Show


		321