|
Just as the total amount of energy within a closed system remains constant, so too does the total amount of momentum. Unlike energy, however, momentum is a vector. This means that conservation of momentum has several interesting and novel implications for subjects ranging from rocketry to billiards, car crashes, and contact sports. 
|
Conservation of momentum
|
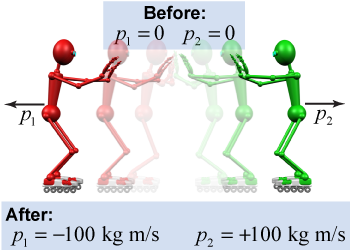Imagine two roller skaters who are stationary. They each have zero momentum. If they push their arms against each other, they will move apart. One skater acquires a momentum to the left, while the other acquires an equal but opposite momentum toward the right. Although each skater’s individual momentum changed, the sum of their momenta did not change!
|
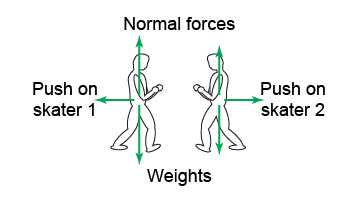Why is this so? Look at these free-body diagrams for the two skaters. Each skater is in equilibrium along a vertical axis—the weight is canceled out by the support force from the floor. When pushing off, however, each skater feels a net force along the horizontal axis. Newton’s third law tells us that these two pushes are action–reaction forces: equal in strength but opposite in direction.
|
|
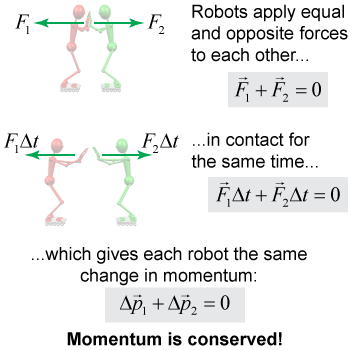
If the two skaters are equally massive, pushing off each other causes equal and opposite accelerations. Now suppose the skaters have different masses. They still feel equal and opposite forces, and these forces act over the same time period, the time interval Δt of their pushing.
| 
|
|
Since force multiplied by time equals impulse, the two skaters experience equal and opposite impulses Δp. In general, if there are no external forces acting on a system, impulses come in pairs that cancel each other out, leaving no net change in the momentum of the system. For a closed system, this implies the law of conservation of momentum:
|
| The total momentum of a closed system remains constant, as long as no net outside force acts upon that system. | Momentum conservation
|
Objects within the closed system—such as the two skaters—are free to exchange momentum between them, but the total momentum cannot change.
 |
Note that the two skaters form a closed system if no outside net force acts upon them. That doesn’t mean that there are no outside forces, period—after all, each skater is supported by a normal force from the ground, and each is weighed down by gravity. The weight and normal forces acting on each skater, however, cancel each other out, adding up to zero net force along a vertical axis. That leaves only the action–reaction forces that the skaters exert upon each other; and that makes the pair of skaters a closed system for purposes of momentum conservation. 
|
| |
|
