|
We often think of Newton’s second law as F = ma. But Newton originally expressed his second law in a way that relates to momentum. Newton defined force as the rate of change of momentum—the change in momentum divided by the time interval. Just as velocity is the rate at which displacement changes, force can be expressed as the rate at which momentum changes. | | | F | = | force (N) | | Δp | = | change in momentum (kg m/s) | | Δt | = | change in time (s) |
| Force
rate of change of momentum |
|
|
Newton’s definition of force in terms of momentum leads to a new quantity: impulse. Multiplying both sides of F = ∆p/∆t by ∆t gives F∆t = ∆p. The product of force and the duration of time the force is applied is called impulse and is usually denoted with the letter J. An impulse applied to an object causes a change in its momentum, ∆p, equal to F∆t.
|
| (11.2) | | | J | = | impulse (kg m/s) | | Δp | = | momentum (kg m/s) | | F | = | force (N) | | Δt | = | time (s) |
| Impulse
force applied over time interval |
|
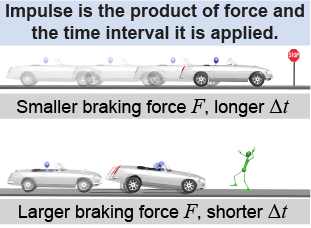The same impulse can be applied through very different forces. Braking gently applies a small force, whereas slamming on the brakes applies a large force; both bring the car to a complete stop, so both apply the same impulse. How else are they different? Braking gently brings the car to a stop over a long time Δt, while slamming on the brakes does so over a short duration Δt. But in both cases the car has changed its momentum from a large value to zero!
|
| Cushioning is an application of this definition of impulse as the product of force and time. When a falling person lands on a hard surface, his momentum changes rapidly—over a short time interval Δt—which means that the applied force is large. If he lands on a cushion, however, the same impulse is now delivered over a longer period of time, so he experiences a much smaller force. One hurts, while the other doesn’t! Car airbags use the same principle. The same phenomenon is also experienced when you bend your legs while landing. Bending your knees extends the amount of time the impulse is applied, thereby reducing the force you experience. If you don’t bend your knees, you can easily break your legs—even when falling from a small height! |
|
As Jane approaches a stop sign, she applies a braking force of 10,000 N. Her car has a mass of 2,000 kg and is moving with a velocity of +20 m/s. What is the impulse imparted to bring the car to a stop? - −400,000 kg m/s
- −40,000 kg m/s
- −4,000 kg m/s
- −400 kg m/s
 |
The answer is b. The imparted impulse equals the car’s change in momentum:
J = pf − pi = 0 − (2,000 kg)(20 m/s) = −40,000 kg m/s. 
|
Using the impulse you found above, how long will it take for Jane’s car to stop? - 4 s
- 40 s
- 0.04 s
- 0.4 s
|
|
The answer is a. Dividing both sides of the expression for impulse by the force and rearranging for time we get Calculating Δt gives
|
