Essential Physics

Solving momentum conservation problems

The law of conservation of momentum is a powerful tool for understanding how objects move after they interact. A rocket expelling exhaust, a car crash on the highway, and the recoil of a hunter’s rifle all involve objects exchanging action–reaction forces. All can be understood by studying momentum. How can we put the law of momentum conservation to work? Read the text aloud

Read the text aloud

Momentum conservation for a two-body system

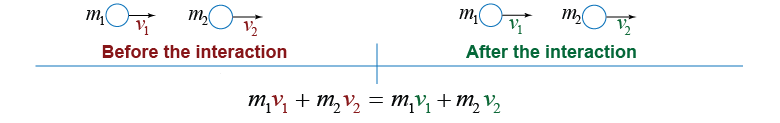
Imagine a system with two objects that can only move to the left or right. They may or may not collide; they may or may not stick together if they do so. It doesn’t matter: The total momentum of any closed system remains unchanged. This rule applies as long as any outside forces on the system add up to zero. Read the text aloud

Read the text aloud

How to solve momentum problems

To solve momentum problems, set up a table showing the momentum of each object, both before and after the objects interact. (Subscripts are often used to identify the two objects or to indicate initial and final values.) If the motion is along a single axis, decide which direction corresponds to positive velocity. Then be sure to assign plus or minus signs accordingly. Read the text aloud

Read the text aloud

Typically you can calculate most of the momenta right away and state a number in kilogram-meters per second. At least one momentum value, however, will contain an unknown variable: the quantity you are trying to solve for. You may need to rearrange the equation. Read the text aloud

Read the text aloud

What is the astronaut's final velocity?

A motionless 100 kg astronaut is holding a 2 kg wrench while on a spacewalk. To get moving, the astronaut throws the wrench forward at a speed of 5 m/s. How fast does the astronaut move backward?

Asked:	astronaut’s final velocity v_a
Given:	masses m_w = 2 kg (wrench) and m_a = 100 kg (astronaut); initial velocity v₀ = 0 (both); final velocity v_w = 5 m/s (wrench)

Relationships:	momentum p = mv; momentum conservation
Solution:	Momentum before equals momentum after: $\begin{matrix} m_{a} v_{0} + m_{w} v_{0} = m_{a} v_{a} + m_{w} v_{w} & \Rightarrow & 0 = \end{matrix} m_{a} v_{a} + m_{w} v_{w}$ Solve for the astronaut’s final velocity: $v_{a} = - \frac{m_{w} v_{w}}{m_{a}} = - \frac{(2 kg) (5 m/s)}{(100 kg)} = - 0.1 m/s$
Answer:	The astronaut moves 0.1 m/s backward (negative direction).

Read the text aloud

Suppose that the astronaut (above) gave the 2 kg wrench a speed of 10 m/s rather than 5 m/s. What effect would this have on her own recoil speed?

It would not change her recoil speed.
It would divide her speed by two (v_a = −0.05 m/s).
It would multiply her speed by 2 (v_a = −0.2 m/s).

Show

The answer is c: it would multiply her speed by 2. Generally speaking, when two bodies are propelled away from each other, doubling one of the speeds will double the other. In this case, this can be seen by inserting the different value for the final wrench velocity, v_w, and solving as before:

\begin{matrix} m_{a} v_{0} + m_{w} v_{0} & = & m_{a} v_{a} + m_{w} v_{w} \\ (100 kg)(0 m/s) + (2 kg)(0 m/s) & = & (100 kg) v_{a} + (2 kg) (10 m/s) \\ 0 & = & (100 kg) v_{a} + 20 kg m/s \end{matrix}

Now we rearrange terms to solve for the unknown quantity, the astronaut’s velocity (v_a):

v_{a} = - \frac{20 kg m/s}{100 kg} = - 0.2 m/s

The astronaut’s recoil speed has doubled.

Suppose that the astronaut (above) had a mass of 50 kg rather than 100 kg (but all other given quantities remain unchanged). What effect would this have on her recoil speed?

It would not change her recoil speed.
It would divide her speed by 2 (v_a = −0.05 m/s).
It would multiply her speed by 2 (v_a = −0.2 m/s).

Show

The answer is c: it would multiply her speed by two. Generally speaking, when two bodies are propelled away from each other, reducing the mass of one object (while leaving everything else unchanged) will increase that object’s recoil velocity. In this case, this can be seen by inserting the different value for the astronaut mass, m_a, and solving as before:

\begin{matrix} m_{a} v_{0} + m_{w} v_{0} & = & m_{a} v_{a} + m_{w} v_{w} \\ (50 kg)(0 m/s) + (2 kg)(0 m/s) & = & (50 kg) v_{a} + (2 kg) (5 m/s) \\ 0 & = & (50 kg) v_{a} + 10 kg m/s \end{matrix}

Now we rearrange terms to solve for the unknown quantity, the astronaut’s velocity (v_a):

v_{a} = - \frac{10 kg m/s}{50 kg} = - 0.2 m/s

The astronaut’s recoil speed has doubled.


		315