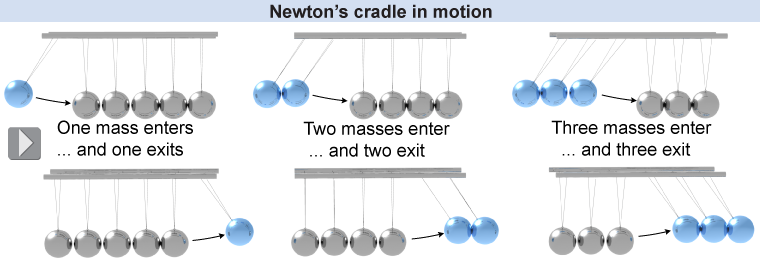
|
If you’ve ever played with a device like the one shown below, you’ve probably asked yourself: “How can it know how many spheres I’ve lifted?” Newton’s cradle, as it’s called, is a row of little pendulums. Each is an identical metal sphere that hangs from two threads or pieces of fishing line. Lift a single sphere at one end of the row and let it drop: One will pop up at the other end. Lift and drop two, and two will leap from the other end. What’s more, the ones that rise up will fall back toward the center and strike the remaining spheres. The cycle will then repeat itself a dozen or more times! 
|
|
|
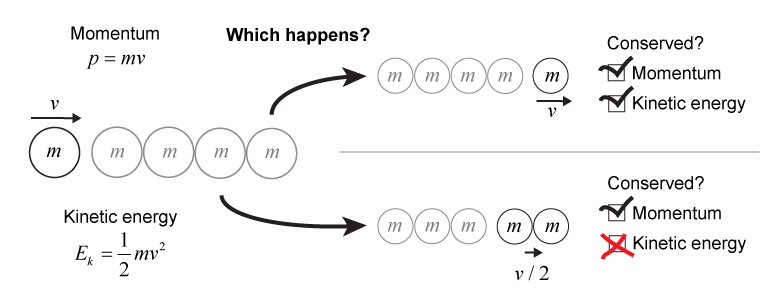
Newton’s cradle is an example of collisions at work. Your first thought might well be, “well, momentum must be conserved, so one ball in means one ball out, both traveling at the same speed.” And you’d be right: Momentum is conserved in Newton’s cradle. But is this the only way for this system to conserve momentum? Couldn’t two balls pop out from the other end, each with half the speed of the one that dropped in, such as in the illustration below?
|
|
Yes, but there’s a catch! A pair of spheres at half the speed has the same momentum as one sphere at full speed. The total kinetic energy of the pair, however, would only be half as much as the single sphere’s. The rest of the kinetic energy would be missing! The collisions in a well-designed Newton’s cradle are nearly elastic, and elastic collisions conserve kinetic energy. There is only one possible outcome that will conserve both momentum and kinetic energy; if one ball swings down at full speed, one and only one ball must pop out, and at full speed.
 |
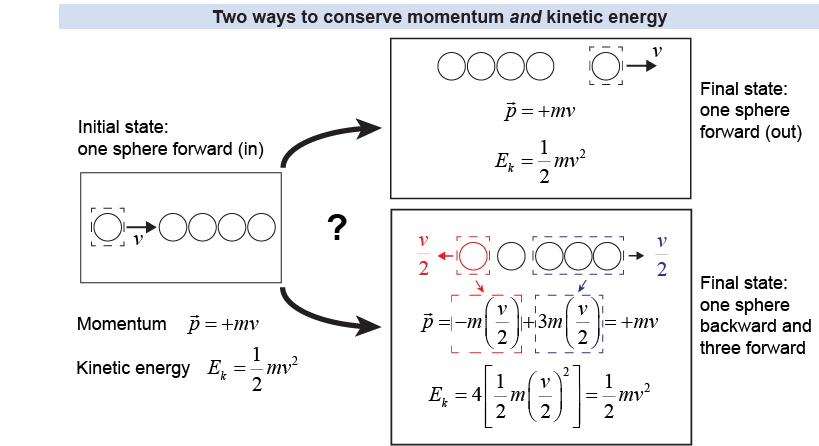It’s true that Newton’s cradle conserves both momentum and kinetic energy, with its “one-in, one-out, two-in, two-out…” behavior. There are other ways, however, to conserve both quantities.
Consider a five-pendulum Newton’s cradle. Imagine that one sphere is lifted on the left end and allowed to fall. If it strikes its partners with velocity +v, it could theoretically bounce back with a new velocity −v/2. If three spheres on the other end flew off together with velocity +v/2, the total momentum and kinetic energy would both be conserved. (Indeed, the situation resembles those you studied with the Investigation on page 320: Select an elastic collision with m1 less than m2.)
Nevertheless, we don’t see this happen! Why not? The incoming sphere is not striking a single larger mass. Rather, it strikes an identical mass, which then strikes another, and so on. When the masses are identical, an elastic collision stops the incoming mass cold and transfers all momentum and kinetic energy to the next. Even if the four target masses are touching one another, the impulse doesn’t accelerate all of them instantly. Rather, it travels at the speed of sound, which is high but not infinite in materials such as steel. 
|
Tape together two of the spheres on one end of Newton’s cradle. Now set it into motion using only one sphere on the other end of the cradle. What happens?
 |
Try it out! 
|
| |
|
