|
Newton’s laws form the foundation for understanding the interaction of forces with objects—such as buildings, bridges, and people. All three laws apply to all situations, all the time. For buildings, bridges, and all other structures that are not supposed to move, the net force is zero—otherwise they would be accelerated. This chapter considers the special case of static equilibrium in which net force is zero. Although there are always forces acting on bridges and buildings, the net force is always zero in a static situation. 
|
Equilibrium of forces
|
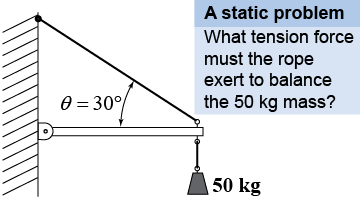In a static problem all the forces acting on an object are in equilibrium and the net force is zero. While equilibrium technically includes the condition of constant velocity, we usually apply equilibrium analysis to things at rest—or things we wish to stay at rest, such as buildings and structures.
|
|
The starting point for any static problem is the assumption of zero net force in every direction. In mathematical language the capital Greek letter sigma (Σ) translates as “the sum of.” The equilibrium of forces is usually written as ΣF = 0 (as in equation 8.1), which translates to “the sum of the forces is zero.” Since force is a vector, this equation applies separately to all three directions.
|
| (8.1) | | | Force
equilibrium
|
|
This compact equation is really three separate equations, one for each direction:
ΣFx = 0 → the sum of forces in the x-direction is zero.
ΣFy = 0 → the sum of forces in the y-direction is zero.
ΣFz = 0 → the sum of forces in the z-direction is zero.
Only a single equation is necessary for 1-D problems, but two equations (x, y) are required for 2-D problems.
|
|
Every force has a direction, magnitude, and point of action, so a free-body diagram is essential to show an object isolated from everything else except for the forces that act on it. A good free-body diagram organizes the information you need in a picture that helps you keep track of the direction, name, and strength of each force.
|
| |
|
