|
Forces from supports or other parts of the structure are often called reactions. Identifying reaction forces is one of the most important steps to solving an equilibrium problem. Start by isolating one or more elements of the structure, alone, in a free-body diagram. Every interaction of each isolated element with other elements or supports is replaced by forces and/or torques. Reactions occur wherever the isolated element touches any other element or any support. 
|
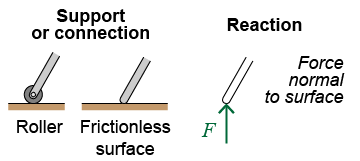A roller or frictionless surface exerts only a normal force at the point of contact. There is only one unknown force and it has a known line of action.
|
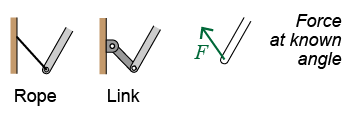A rope or link exerts a force with a known line of action and therefore also has only one unknown force.
|
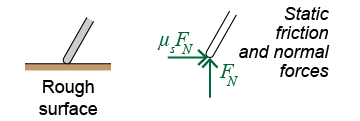A rough (frictional) surface or sliding connection includes the force of friction parallel to the surface and a normal force. There is only one unknown force if the coefficient of static friction μs is given.
|
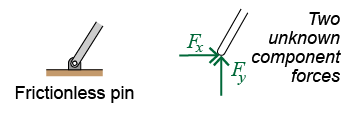A frictionless pin connection exerts reaction forces in two directions (x and y), so there are two unknown forces. The pin indicates that the connection is free to rotate; as a result, there is no reaction torque generated by the support. Many problems are approximately solved by assuming a pinned connection.
|
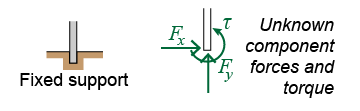The most complex connection is a fixed support that can transmit both forces and torques. As with forces, Newton’s first law also applies to torque. Any torque created by the structure on the support creates an equal and opposite reaction torque that acts on the structure. There are two unknown forces and one unknown torque.
|
|
These diagrams show what kinds of support reactions are created for all of the problems you will encounter in this course—and some for future study too! The fixed support is the most difficult because there are three unknowns: two forces and a torque. Static problems with fixed supports are addressed in more advanced courses.
|
