| | Essential questions | | How do we predict when something will move or not?
How do we determine forces we cannot measure? | |
|
Objects remain at rest only when the net force and the net torque are zero. The converse is also true: if an object remains at rest, then you know the net force and the net torque must be zero. The first statement predicts whether an object will remain at rest or begin to move, while the second statement is used to determine unknown forces. 
|
Part 1: A simply supported beam
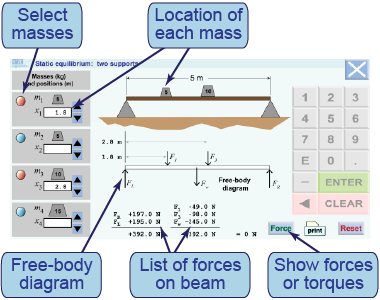
- This interactive model allows you to place up to four masses on a beam that is supported at its ends. You can adjust the placement of the masses by entering distances for each one.
- [Reset] clears all the masses and distances.
- The [Force] or [Torque] button toggles between displaying the force or torque diagrams below the bar.
- What is the relationship between the upward and downward forces on the free-body diagram?
- What is the relationship between the clockwise and counterclockwise torques when measuring torques?
- Use the masses to create an equilibrium in which a force scale under the left support will measure a force of close to 300 N.

|
In this interactive simulation, you will explore free-body force diagrams for static equilibrium.
|
Going further: A lever
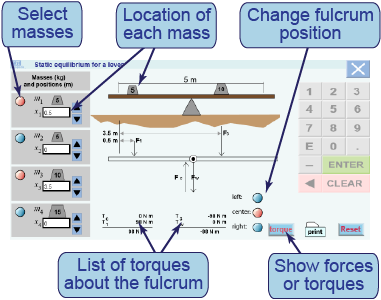
- The interactive model allows you to place the same four masses on a lever that is free to tip one way or the other.
- [Reset] clears all the masses and distances.
- The [Force] or [Torque] button toggles between displaying the force or torque diagrams below the bar.
- Why is the lever harder to balance than the beam in Part 1?
- Why can the lever not be balanced when the fulcrum is on one end?
- How can the direction of tipping be predicted?
- Try to create a situation in which the net torque is +100 N m and another situation in which the net torque is −100 N m. What happens to the lever in each case? Does it tip clockwise or counterclockwise?
|
In this interactive simulation, you will explore static equilibrium using a simple lever similar to a see-saw found in playground equipment.
|
Part 2: Find the unknown mass using static equilibrium
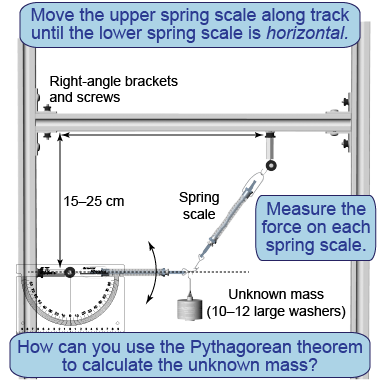
- Attach a long, vertical track to a short, horizontal track using the brackets and screws.
- Attach the protractor and one spring scale to a pin located 15–25 cm below the horizontal track. Attach the other spring scale to a sliding pin on the horizontal track.
- Attach an unknown, hanging mass of 10–12 large washers to the two spring scales.
- Move the upper spring scale along the track until the lower spring scale is horizontal.
- For each spring scale, measure and record the force.
- Draw a free-body diagram for the hanging mass.
- What is the
horizontal component of the force exerted by the upper spring scale? - Use the Pythagorean theorem to calculate the
vertical force exerted on the upper spring scale. - What is the value of the unknown mass? Use a triple beam balance to measure its mass. How well does your value agree? Explain any discrepancies.

|
Going further: Using trigonometry to find the unknown mass
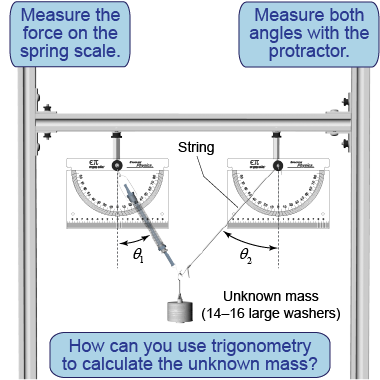
- Attach a spring scale to the horizontal track. Clamp a string to a second sliding pin.
- Suspend a hanging mass of 14–16 large washers from the spring scale and string.
- Slide the pins along the track until the mass is well balanced and the spring scale acts at an angle of approximately 30° from vertical.
- Measure and record the force, and the angle the spring scale makes with the horizontal.
- Draw a free-body diagram for the hanging mass.
- Using the force and angle for the spring scale, calculate the string force and its
vertical force component. - What is the net horizontal force? What must be the horizontal force applied by the string?
- Using the angle of the string, calculate the string force and the
vertical force for the string. - What is the net
vertical force? What must be the weight of the hanging mass? - What is the value of the unknown mass? Use a triple beam balance to measure its mass. How well does your value agree? Explain any discrepancies.
| | |
| |
|

