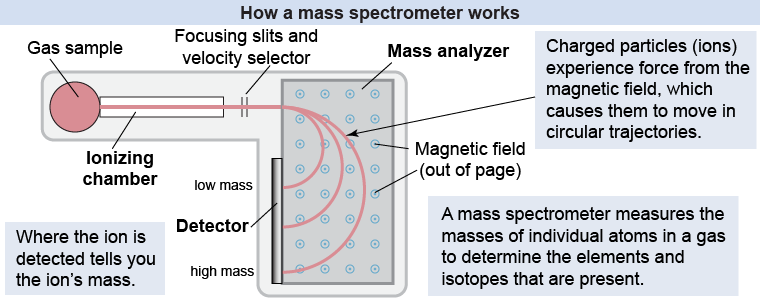
|
The mass spectrometer is a scientific instrument used to identify the elements and isotopes present in a gas. Inside the mass spectrometer, magnetic forces on moving charged particles are used to measure the masses of individual atoms. How does it work? 
|
|
In the ionizing chamber, atoms are ionized (into positive ions) by removing one (or more) of their outermost electrons. Ions of a particular velocity are isolated in the velocity selector and then emerge in a narrow beam as a result of focusing slits. In the mass analyzer, these moving charges pass through a strong magnetic field. The atoms experience a magnetic force that causes them to move in circles; the radius of the circle depends on the mass of the ion. Ions of different masses will strike different parts of the detector—allowing you to determine their masses.
 |
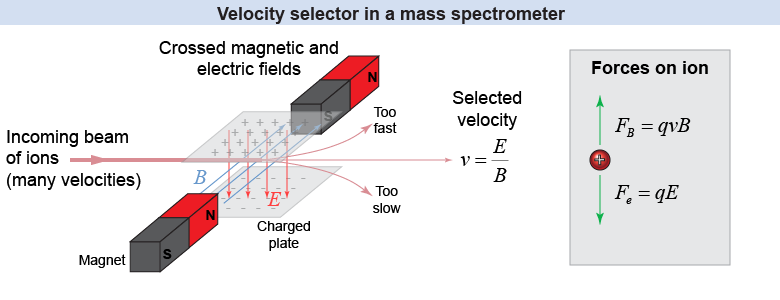Ions emerge from the ionizing chamber traveling at a range of velocities. But the mass analyzer unit of the spectrometer requires all the ions to have approximately the same velocity—otherwise, ions of the same charge and mass will have different cyclotron radii. The velocity selector in a mass spectrometer allows only those ions within a narrow, selected range of velocities to pass through into the mass analyzer. The velocity selector contains two fields, one electric and one magnetic, that are aligned at right angles to each other and to the direction of the beam of ions. The ion experiences a magnetic force in one direction (such as upward) and an electric force in the opposite direction (e.g., downward). The electric and magnetic fields are tuned to precise values that will cause the electric and magnetic forces to cancel only for ions of a particular velocity; ions of other velocities experience net forces that cause them to move upward or downward. Since the electric force on the ion is Fe = qE and the magnetic force is FB = qvB (where θ = 90°), the two forces are equal when The selected velocity v will be used to calculate the mass of the ion at the bottom of this page. 
|
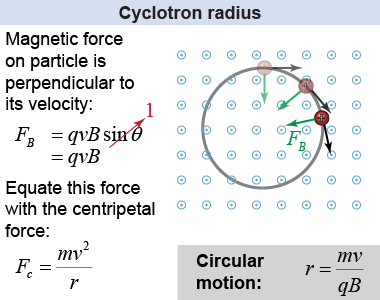According to the right-hand rule, the magnetic field exerts a force on the ions that is always perpendicular to their velocity. As you learned on page 209, a constant force applied perpendicular to the object’s velocity will result in circular motion! The radius of circular motion for a charged particle in a uniform magnetic field is referred to as the cyclotron radius (or gyroradius). This is the explanation behind the circular tracks in the bubble chamber on the previous page.
|
The cyclotron radius can be calculated by using equation (19.4) and the equation for the centripetal force. Set the centripetal force Fc = mv2/r equal to the magnetic force on the ions, FB = qvB (where sin θ = 1, because the field is perpendicular to the velocity), then solve for the mass of the ions to obtain equation (19.5). | (19.5) | | | r | = | radius of trajectory (m) | | q | = | charge of particle (C) | | B | = | magnetic field strength (T) | | v | = | particle speed (m/s) | | m | = | particle mass (kg) |
| Mass of an ion
given its gyroradius |
The mass of the ion is therefore proportional to the radius of curvature of its trajectory through the mass analyzer. That’s how the mass spectrometer works!
|
|
Mass spectroscopy has many applications all across the physical sciences. In the periodic table of the elements, the mass of each element is listed as the average mass of its isotopes. The relative abundances of each isotope can be measured with a mass spectrometer, and then a mathematical average taken of each isotope’s mass to obtain the average value. A mass spectrometer can be used to measure the abundance of the carbon-14 isotope relative to carbon-12 and carbon-13 in the carbon dating method. Mass spectrometers are also used in various space missions to measure the relative abundances of elements, such as on the Curiosity Rover that landed on Mars in 2012. Finally, mass spectroscopy can be used to look for contaminants in a gas.
|
Why do more massive ions move along trajectories with larger radii than lower mass ions?
 |
More massive ions have greater inertia. Since a = F/m, more massive ions experience a smaller acceleration. The centripetal acceleration is a = v2/r (from Chapter 7), so a smaller acceleration corresponds to a larger radius. Therefore, the massive ions move in a larger radius. 
|
