|
Electricity and magnetism are related to each other: Moving electric charges, or electric current, generates a magnetic field. Can you reverse this process, using a magnet to create an electric current? If you placed a magnet inside a solenoid, would a current be produced in the wire? The phenomenon at the heart of this question is electromagnetic induction, which is the principle behind electric generators in power plants—as well as transformers that convert electricity to high voltages for long-distance transmission. 
|
Magnetic flux through a loop of wire
|
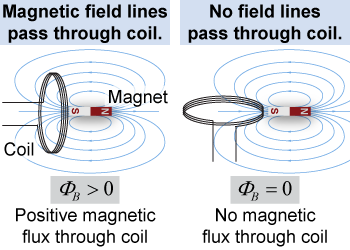The direction and strength of a bar magnet’s magnetic field can be visualized by using field lines, as you learned on page 514. The strength of the magnetic field passing through a wire coil determines the magnetic flux. When the imaginary surface formed by the coil is perpendicular to the magnetic field, many field lines pass through the coil and there is a large magnetic flux through it. When the coil’s surface is parallel to the field, no lines pass through it and it has zero magnetic flux. Magnetic flux depends on the strength of the field, the area of the coil, and the relative orientation between the field and the coil, as shown in equation (19.1).
|
| (19.1) | | | ΦB | = | magnetic flux (T m2) | | B | = | magnetic field (T) | | A | = | area of loop (m2) | | θ | = | angle between field and normal (deg) |
| Magnetic flux
through a wire loop |
|
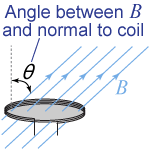Since ΦB is the product of magnetic field (measured in tesla or T) and area (measured in square meters), the units of ΦB are T m2, which is also called the weber (Wb). Be careful in determining the angle θ between the magnetic field and the normal to the surface of the coil—as you can see both in the illustration at right and in the solved problem below.
|
A 0.5 cm square wire loop inside a generator lies between the poles of two magnets, as shown in the figure at right. If the magnetic field strength is 0.1 T, what is the magnetic flux through the loop? | Asked: | magnetic flux ΦB | | Given: | loop dimensions l = 0.5 cm by w = 0.5 cm; magnetic field B = 0.1 T | | Relationships: | | ΦB = BA cos θ | area = A = l × w |
angle between magnetic field and normal to wire loop θ = 90°−30° = 60° | | Solution: | | | Answer: | ΦB = 1.25 × 10−6 T m2 = 1.25 × 10−6 Wb |
|
Using equation (19.1), explain why the magnetic flux is zero when a wire coil’s surface is parallel to a magnetic field.
 |
When the coil’s surface is parallel to the magnetic field, the angle between the surface and the field is 0°. The angle between the normal and the magnetic field is therefore 90°. In equation (19.1), the value of cos θ = cos 90° = 0, so the magnetic flux is also zero. 
|
