|
Particle physicists use “bubble chambers” (or more modern spark chambers) to track the paths of colliding elementary particles—protons, electrons, and other subatomic particles. In the collision illustrated at right, two of the particles that were created follow spiral trajectories. Why do these particles travel along spiral paths in a bubble chamber? The answer has to do with electromagnetism. The same phenomenon is used in older television sets to create the picture on the screen! 
|
Magnetic force on a moving electric charge
|
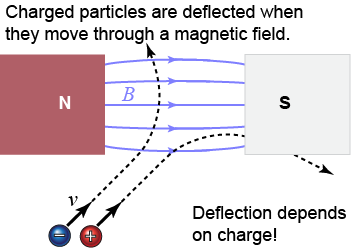At the beginning of this chapter, you learned that moving electric charges—also called electric current—create a magnetic field around them. It is also the case that an electric charge will feel force when moving in a magnetic field. This magnetic force depends not only on the strength of the magnetic field B but also on the charge q of the particle. Moving positive charges feel a magnetic force in one direction, whereas negative charges with the same velocity will feel a force in the opposite direction. Neutral particles, such as neutrons, feel no magnetic force at all! Furthermore, the strength of the magnetic force depends on how fast the charged particle is moving. Slow particles feel only a weak force, whereas high-speed particles feel a strong force. Equation (19.4) gives the force on a charged particle in a magnetic field.
|
| (19.4) | | | FB | = | magnetic force (N) | | q | = | electric charge (C) | | v | = | speed (m/s) | | B | = | magnetic field (T) | | θ | = | angle between velocity and field (deg) |
| Magnetic force
on a moving charge |
|
The direction of the magnetic force is determined by the right-hand rule. You have seen other right-hand rules before for the magnetic field around a current-carrying wire and the magnetic field of an electromagnet! In this case, your thumb represents the direction of the velocity, your index finger the direction of the magnetic field, and your middle finger the direction of the resulting magnetic force on a positively charged particle. Negative charges will feel a force in the opposite direction.
|
|
The magnetic force has a property that is very different from gravity or the electric force. Two masses that are separated by 1 m feel the same mutual gravitational attraction, regardless of the direction or magnitude of their velocity vectors. Likewise, two electric charges exert the same electric force on each other (from Coulomb’s law), regardless of their velocities. But the magnitude and direction of the magnetic force felt by a moving charged particle depends on the magnitude and direction of its velocity.
|
What is the magnetic force on a particle with charge −3.0×10−5 C that is moving at 3.9×104 m/s parallel to the field lines of a magnetic field whose strength is 6.8×10−3 T?
 |
The answer is zero! The problem states that the charged particle is moving parallel to the field lines of the magnetic field. The words “parallel to the field lines” means that the angle θ between the particle’s velocity and the field lines is zero; therefore, sin θ is also zero. The magnetic force is then FB = qvB sin θ = 0.
Charged particles moving parallel to magnetic field lines experience no magnetic force! If instead the particle was moving perpendicular to the field, the magnitude of the force on it would be 8.0 × 10−3 N. 
|
