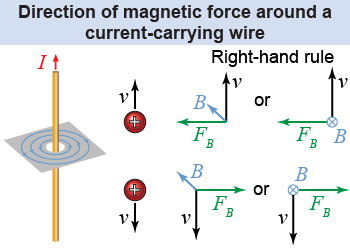|
When a straight wire carries an electric current, you learned on page 548 that it creates a magnetic field surrounding it in concentric circles. This magnetic field can exert a magnetic force on nearby moving charged particles. Earlier, you learned the right-hand rule to determine the direction of magnetic force on a moving charged particle. Using the right-hand rule in the illustration at right, you can see that a positively charged particle moving in the same direction as the electric current will feel a magnetic force toward the wire. Likewise, a positively charged particle moving in the opposite direction as the electric current will feel a magnetic force away from the wire. 
 |
It is probably worth a reminder on the notation for vectors drawn into or out of the page of this book (or your computer’s screen). When a vector quantity, such as magnetic field , is directed into or out of the page, the symbols at left are used to denote its direction. These symbols use the “arrow” metaphor: A vector coming out of the page looks like an arrowhead, while a vector going into the page looks like the crossed feathers at the end of an arrow. 
|
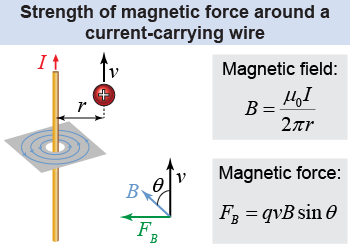If the direction of the magnetic force is given by the right-hand rule, what is the magnitude or strength of the magnetic field and force? The magnitude of the magnetic field around a straight, current-carrying wire is given by equation (19.6). The magnetic field B is stronger for a larger electric current I and becomes weaker as the distance r from the wire increases.
|
| (19.6) | | | B | = | magnetic field (T) | | μ0 | = | permeability constant = 4π×10−7 T m/A | | I | = | current (A) | | r | = | distance from wire (m) |
| Magnetic field
around a
current-carrying wire |
|
|
Once the magnitude of the magnetic field is known, the magnetic force can be calculated by using equation (19.4), or FB = qvB sin θ, where θ is the angle between the magnetic field and velocity vectors.
|
|
In equation (19.6), most of the quantities are familiar: magnetic field B, measured in teslas (T); electric current I, in amperes; and distance r from the wire , in meters. What is μ0? It is called the permeability of free space, which is a physical constant describing how effectively a magnetic field can be established in a vacuum. (It is sometimes called the vacuum permeability.) But all you really need to know to use equation (19.6) is that μ0 is a physical constant equal to 4π×10−7 T m/A!
|
|
On a deeper level, the permeability of a material is its ability to support the formation of a magnetic field within itself. The vacuum permeability (also called the “permeability of free space” or the “permeability constant”) is the magnetic permeability of a vacuum and is denoted by μ0. That μ0 is not equal to zero means that a vacuum can still support a magnetic field, even though it is empty space! Later in Chapter 22, you will learn that light is composed of oscillating electric and magnetic fields and that light can propagate in a vacuum. Light can only propagate through a vacuum because μ is not zero in a vacuum!
|
Calculate the magnetic field 10 cm away from a straight wire carrying 2 A of current. | Asked: | magnetic field B | | Given: | distance r = 0.1 m; electric current I = 2 A | | Relationships: | B = μ0I/(2πr) | | Solution: | | | Answer: | B = 4 × 10−6 T = 4 μT |
|
An average value of the Earth’s magnetic field is 5×10−5 T. How far away from a wire carrying 1 A of current does the magnitude of the wire’s magnetic field equal the Earth’s magnetic field?
 |
Asked: distance r from wire
Given: Earth’s magnetic field B = 5×10−5 T
Relationships: permeability constant μ0 = 4π×10−7 T m A−1 Solve: Using the magnetic field equation, we want to solve for the distance r from the wire. First, multiply both sides by r: Then divide both sides by the magnetic field B to obtain the expression for r: Now calculate the answer using the values in the problem: Answer: The magnetic field from the wire equals the magnitude of the Earth’s magnetic field at a distance of 4 mm from the wire. 
|
